一个物体从斜面上高h处由静止滑下并紧接着在水平面上滑行一段距离后停止,测得停止处对开始运动处的水平距离为s,如图所示,不考虑物体滑至斜面底端的碰撞作用,并设斜面与水平面对物体的动摩擦因数相同,求动摩擦因数μ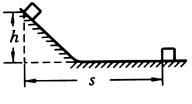
如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5 m,电阻忽略不计,其上端接一小灯泡,电阻为1 Ω。一导体棒MN垂直于导轨放置,质量为0.2 kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5。在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为0.8 T。将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为多少?(重力加速度g取10 m/s2,sin 37°=0.6)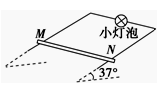
矩形线框abcd的边长分别为l1、l2,可绕它的一条对称轴OO′转动,线框电阻为R,转动角速度为ω。匀强磁场的磁感应强度为B,方向与OO′垂直,初位置时线圈平面与B平行,如图所示。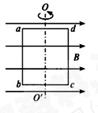
(1)以图示位置为零时刻,写出现框中感应电动势的瞬时值表达式。
(2)由图示位置转过90°的过程中,通过线框截面的电荷量是多少?
如图所示,一个光滑的圆弧形槽半径为R,圆弧所对的圆心角小于5°.AD的长为s,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?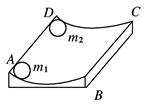
一列简谐波沿x轴方向传播,已知x轴上x1=0和x2="1" m两处质点的振动图象分别如图(甲)、(乙)所示,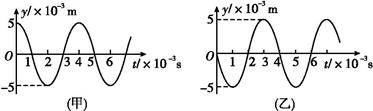
求(1)若此波沿x轴正向传播,则波的传播速度的可能值.
(2)若此波沿x轴负向传播,则波的传播速度的可能值.
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,介质中质点P、Q分别位于x="2" m、x="4" m处.从t=0时刻开始计时,当t="15" s时质点Q刚好第4次到达波峰.
(1)求波速;
(2)写出质点P做简谐运动的表达式.