、(本小题满分9分)已知函数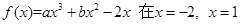 处取得极值。(1)求函数
处取得极值。(1)求函数 的解析式;
的解析式;
(2)求函数 的单调区间
的单调区间
已知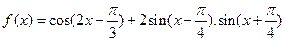
(1)求函数f(x)的最小正周期和图像的对称轴方程;
(2)求函数f(x)在区间 上的值域。
上的值域。
设全集是实数集R,A= B=
B=
(1)当a=-4时,求A∩B和A∪B;
(2)若( )∩B=B,求实数a的取值范围。
)∩B=B,求实数a的取值范围。
设函数的定义域为(0,+∞),且对任意正实数x,y都有f(x·y)=f(x)+f(y)恒成立,已知f(2)=1且x>1时f(x)>0.
(1)求 ;
;
(2)判断y=f(x)在(0,+ ∞)上的单调性;
(3)一个各项均为正数的数列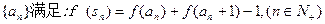 其中sn是数列
其中sn是数列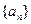 的前n项和,求
的前n项和,求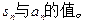
已知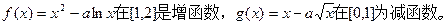
(1)求f(x),g(x)的表达式;
(2)求证:当x>0时,方程f(x)=g(x)+2有唯一解。
设f(x)=
(1)求证:函数y=f(x)与g(x)的图像有两个交点;
(2)设f(x)与g(x)的图交点A、B在x轴上的射影为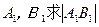 的取值范围。
的取值范围。