观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中共有5个正方形,第3个图中共有14个正方形,按照这种的规律可知第5个图形共有________个正方形。 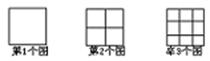
如图,在⊙O上位于直径AB的异侧有定点C和动点P,AC=AB,点P在半圆弧AB上运动(不与A、B两点重合),过点C作直线PB的垂线CD交PB于D点.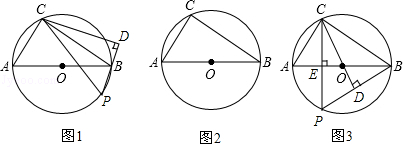
(1)如图1,求证:△PCD∽△ABC;
(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由;
(3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数.
如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使B点与C点重合,得到△DCE,连接BD,交AC于F.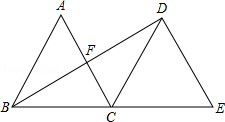
(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.
节约能源,从我做起.为响应长株潭“两型社会”建设要求,小李决定将家里的4只白炽灯全部换成节能灯.商场有功率为10w和5w两种型号的节能灯若干个可供选择.
(1)列出选购4只节能灯的所有可能方案,并求出买到的节能灯都为同一型号的概率;
(2)若要求选购的4只节能灯的总功率不超过30w,求买到两种型号的节能灯数量相等的概率.
为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,莲城中学对八年级部分学生就一期来“分组合作学习”方式的支持程度进行调查,统计情况如图.试根据图中提供的信息,
回答下列问题:
(1)求本次被调查的八年级学生的人数,并补全条形统计图;
(2)若该校八年级学生共有180人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?
已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.