如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。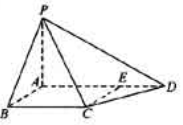
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积
已知函数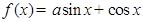 ,其中
,其中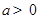 .
.
(Ⅰ)当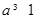 时,判断
时,判断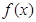 在区间
在区间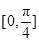 上的单调性;
上的单调性;
(Ⅱ)当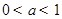 时,若不等式
时,若不等式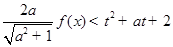 对于
对于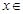
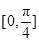 恒成立,求实数
恒成立,求实数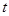 的取值范围.
的取值范围.
已知椭圆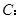
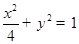 ,
,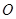 为坐标原点,直线
为坐标原点,直线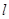 与椭圆
与椭圆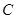 交于
交于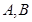 两点,且
两点,且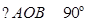 .
.
(Ⅰ)若直线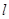 平行于
平行于 轴,求
轴,求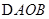 的面积;
的面积;
(Ⅱ)若直线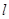 始终与圆
始终与圆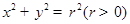 相切,求
相切,求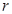 的值.
的值.
如图,在矩形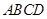 中,
中, ,
,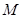 为
为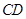 的中点.将
的中点.将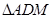 沿
沿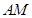 折起,使得平面
折起,使得平面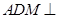 平面
平面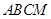 .点
.点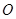 是线段
是线段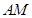 的中点.
的中点.
(Ⅰ)求证:平面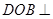 平面
平面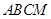 ;
;
(Ⅱ)求证: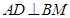 ;
;
(Ⅲ)过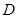 点是否存在一条直线
点是否存在一条直线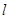 ,同时满足以下两个条件:
,同时满足以下两个条件:
①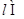 平面
平面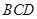 ;②
;②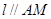 .
.
请说明理由.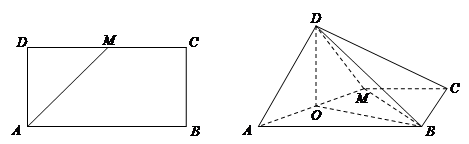
某学科测试,要求考生从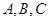 三道试题中任选一题作答.考试结束后,统计数据显示共有420名学生参加测试,选择
三道试题中任选一题作答.考试结束后,统计数据显示共有420名学生参加测试,选择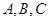 题作答的人数如下表:
题作答的人数如下表:
| 试题 |
 |
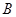 |
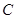 |
| 人数 |
180 |
120 |
120 |
(Ⅰ)某教师为了解参加测试的学生答卷情况,现用分层抽样的方法从420份试卷中抽出若干试卷,其中从选择 题作答的试卷中抽出了3份,则应从选择
题作答的试卷中抽出了3份,则应从选择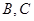 题作答的试卷中各抽出多少份?
题作答的试卷中各抽出多少份?
(Ⅱ)若在(Ⅰ)问被抽出的试卷中,选择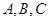 题作答得优的试卷分别有2份,2份,1份.现从被抽出的选择
题作答得优的试卷分别有2份,2份,1份.现从被抽出的选择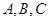 题作答的试卷中各随机选1份,求这3份试卷都得优的概率.
题作答的试卷中各随机选1份,求这3份试卷都得优的概率.
已知递增的等差数列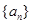 (
(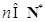 )的前三项之和为18,前三项之积为120.
)的前三项之和为18,前三项之积为120.
(Ⅰ)求数列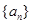 的通项公式;
的通项公式;
(Ⅱ)若点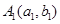 ,
,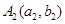 ,…,
,…,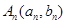 (
(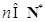 )从左至右依次都在函数
)从左至右依次都在函数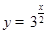 的图象上,求这
的图象上,求这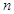 个点
个点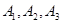 ,…,
,…,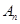 的纵坐标之和.
的纵坐标之和.