.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为
A. |
B. |
C.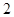 |
D. |
已知双曲线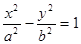
 的左右焦点分别为
的左右焦点分别为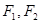 ,若双曲线右支上存在一点
,若双曲线右支上存在一点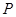 ,使得
,使得 关于直线
关于直线 的对称点恰在
的对称点恰在 轴上,则该双曲线的离心率
轴上,则该双曲线的离心率 的取值范围为()
的取值范围为()
A.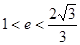 |
B.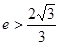 |
C. |
D.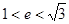 |
近期由于雨雪天气,路况不好,某人驾车遇到紧急情况而刹车,以速度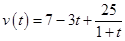 (
( 为时间单位s)行驶至停止.在此期间汽车继续行驶的距离(单位;
为时间单位s)行驶至停止.在此期间汽车继续行驶的距离(单位; )是()
)是()
A.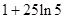 |
B.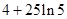 |
C. |
D. |
已知在 中,边
中,边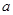 、
、 、
、 的对角为
的对角为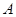 、
、 、
、 ,
, ,
, ,
, ,则此三角形中边
,则此三角形中边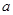 的取值使得函数
的取值使得函数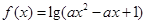 的值域为
的值域为 的概率为()
的概率为()
A. |
B. |
C.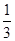 |
D. |
在如图所示的空间直角坐标系 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(2,1,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的侧视图和俯视图分别为()
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(2,1,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的侧视图和俯视图分别为()

| A.①和② | B.①和③ | C.③和② | D.④和② |
已知等比数列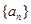 的首项
的首项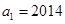 ,公比为
,公比为 ,记
,记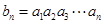 ,则
,则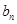 达到最大值时,
达到最大值时,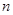 的值为()
的值为()
A.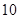 |
B.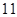 |
C.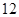 |
D.不存在 |