如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究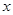 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
如图,在等腰Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H。判断四边形AHBG的形状。
如图,E是平行四边形ABCD中AB延长线上一点,ED交BC于F,求证: 。
。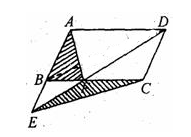
已知:如图,在平行四边形ABCD中,点E、F在AC上,且AE=DF.
求证:四边形BECF是平行四边形.
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.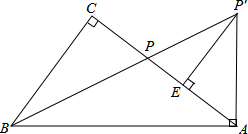
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当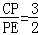 ,BP′=5
,BP′=5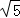 时,求线段AB的长.
时,求线段AB的长.
如图1,在△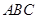 中,
中,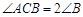 ,
,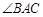 的平分线
的平分线 交
交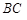 于点
于点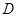 ,点
,点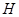 为
为 上一动点,过点
上一动点,过点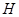 作直线
作直线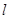 ⊥
⊥ 于
于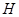 ,分别交直线
,分别交直线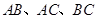 于点
于点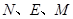 .
.

(1)当直线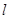 经过点
经过点 时(如图2),证明:
时(如图2),证明: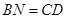 ;
;
(2)当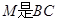 中点时,写出
中点时,写出 和
和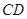 之间的等量关系,并加以证明;
之间的等量关系,并加以证明;