质点做直线运动的v-t图象如图所示,初速度为ν0,末速度为ν1,则时间t1内的平均速度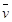 为( )
为( )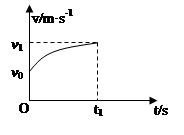
A.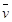 < < |
B.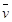 = = |
C.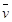 > > |
| D.无法比较 |
汽车以一定速率通过拱桥时,下列说法中正确的是()
| A.在最高点汽车对桥的压力大于汽车的重力 |
| B.在最高点汽车对桥的压力等于汽车的重力 |
| C.在最高点汽车对桥的压力小于汽车的重力 |
| D.汽车以恒定的速率过桥时,汽车所受的合力为零 |
如图在固定的圆锥形漏斗的光滑内壁上,有两个质量相等的小球A和B,它们分别紧贴漏斗的内壁,在不同的水平面上做匀速圆周运动.则以下叙述中正确的是()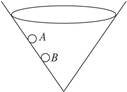
| A.A的线速度大于B的线速度 |
| B.A的角速度大于B的角速度 |
| C.A对漏斗内壁的压力大于B对漏斗内壁的压力 |
| D.A的周期大于B的周期 |
火车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定.若在某转弯处规定行驶速度为v,则下列说法中正确的是()
①当以速度v通过此弯路时,火车重力与轨道支持力的合力提供向心力②当以速度v通过此弯路时,火车重力、轨道支持力和外轨对轮缘弹力的合力提供向心力③当速度大于v时,轮缘挤压外轨④当速度小于v时,轮缘挤压外轨
| A.①③ | B.①④ | C.②③ | D.②④ |
在水平路面上安全转弯的汽车,向心力是()
| A.重力和支持力的合力 |
| B.重力、支持力和牵引力的合力 |
| C.汽车与路面间的静摩擦力 |
| D.汽车与路面间的滑动摩擦力 |
关于在公路上行驶的汽车正常转弯时,下列说法中正确的是()
| A.在内外侧等高的公路上转弯时的向心力由静摩擦力提供 |
| B.在内外侧等高的公路上转弯时的向心力由滑动摩擦力提供 |
| C.在内侧低、外侧高的公路上转弯时的向心力可能由重力和支持力的合力提供 |
| D.在内侧低、外侧高的公路上转弯时的向心力可能由重力、摩擦力和支持力的合力提供 |