在平面直角坐标系xoy中，已知曲线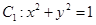
，将
上的所有点的横坐标、纵坐标分别伸长为原来的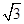
、2倍后得到曲线
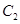，以平面直角坐标系xoy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线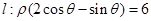
（1） 试写出直线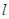
的直角坐标方程；
（2） 在曲线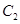上求一点P，使点P到直线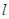的距离最大，并求出此最大值。
（本小题满分12分）
已知函数
，
（1）若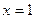
为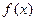
的极值点，求
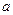的值；
（2）若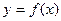
的图象在点（1，
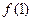）处的切线方程为
，求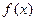在区间[-2, 4]上的最大值。
（3）当
时，若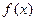在区间（-1，1）上不单调，求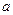的取值范围。
（本小题满分12分）
求曲线的方程：
（1）求中心在原点，左焦点为
，且右顶点为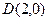
的椭圆方程；
（2）求中心在原点，一个顶点坐标为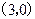
，焦距为10的双曲
线方程。
（本小题满分
12分）
某运动员进行20次射击练习，记录了他射击的有关数据，得到下表：
| 环数 |
7 |
8 |
9 |
10 |
| 命中次数 |
2 |
7 |
8 |
3 |
（1）求此运动员射击的环数的平均值；
（2）若将表中某一环数所对应的命中次数作为一个结果，在四个结果（2次、7次、8次、3次）中，随机取2个不同的结果作为基本事件进行研究，记这两个结果分别为
次、
次，每个基本事件为
，求事件
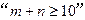的概率。
（本小题满分12分）
已知函数
，
（1）求函数
的定义域；（2）证明：是偶函数；
（3）若
，求
的取值范围。
（本小题满分12分）
已知集合
（1）求
和
；（2）写出集合
的所有子集。