平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设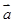 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an), =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量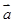 与
与 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ= .已知n维向量
.已知n维向量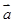 ,
, ,当
,当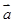 =(1,1,1,1,…,1),
=(1,1,1,1,…,1), =(-1,-1,1,1,1,…,1)时,cosθ等于______________
=(-1,-1,1,1,1,…,1)时,cosθ等于______________
在数列{an}中, ,当n为正奇数时,
,当n为正奇数时,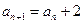 ;当n为正偶
;当n为正偶 数时,
数时, ,则
,则
已知角 的终边过点(4,-3),则
的终边过点(4,-3),则 =
=
(本小 题满分12分)
题满分12分)
设
 为奇函数,其图象在点
为奇函数,其图象在点
 处的切线与直线
处的切线与直线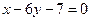 垂直,导函数
垂直,导函数 的最小值为
的最小值为
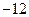 .
.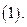 求
求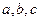 的值
的值 .求函数
.求函数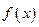 的单调递增
的单调递增 区间,极大值和极小值,并求函数
区间,极大值和极小值,并求函数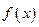 在
在 上的最大值与最小值.
上的最大值与最小值.
(本小题满分12分)
应用题:提高过江大桥的车辆通行能力可改善整个城市的交通状况. 在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵
在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵 塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流
塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流 速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函
速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函 数v(x)的表达式.
数v(x)的表达式.
(本小题满分12分)
袋中有 个白球和
个白球和 个黑球,每次从中任取
个黑球,每次从中任取 个球
个球 ,每次取出黑球后不再放
,每次取出黑球后不再放 回去,直到取出白球为止.求取球次数
回去,直到取出白球为止.求取球次数 的分布列,并求出
的分布列,并求出 的期望值和方差.
的期望值和方差.