出租司机小张某天下午的营运全是在到西走向的大街上进行的,若规定向东为正,向西为负,他这天下午行车里程(单位:千米)记录如下: +8,-3,+15,-10,-13,+3,-15,+11,-12
(1)将最后一名乘客送到目的地时,小张距下午出车点的距离是多少千米?
(2)若汽车耗油量为0.08升/千米,这天下午汽车共耗油多少升?
在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从A地沿相同路线骑行去距A地30千米的B地,已知甲骑行的速度是乙的1.2倍.
(1)若乙先骑行2千米,甲才开始从A地出发,则甲出发半小时恰好追上乙,求甲骑行的速度;
(2)若乙先骑行20分钟,甲才开始从A地出发,则甲、乙恰好同时到达B地,求甲骑行的速度.
已知一次函数 的图象与反比例函数 的图象相交于点 , .
(1)求一次函数的表达式,并在图中画出这个一次函数的图象;
(2)根据函数图象,直接写出不等式 的解集;
(3)若点C是点B关于y轴的对称点,连接AC,BC,求△ABC的面积.

公司生产A、B两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的A、B型扫地机器人中各随机抽取10台,在完全相同条件下试验,记录下它们的除尘量的数据(单位:g),并进行整理、描述和分析(除尘量用 表示,共分为三个等级:合格 ,良好 ,优秀 ),下面给出了部分信息:
10台A型扫地机器人的除尘量:83,84,84,88,89,89,95,95,95,98.
10台B型扫地机器人中“良好”等级包含的所有数据为:85,90,90,90,94
抽取的A、B型扫地机器人除尘量统计表
|
型号 |
平均数 |
中位数 |
众数 |
方差 |
“优秀”等级所占百分比 |
|
A |
90 |
89 |
a |
26.6 |
40% |
|
B |
90 |
b |
90 |
30 |
30% |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)这个月公司可生产B型扫地机器人共3000台,估计该月B型扫地机器人“优秀”等级的台数;
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).

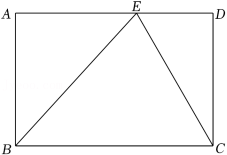
在学习矩形的过程中,小明遇到了一个问题:在矩形ABCD中,E是AD边上的一点,试说明△BCE的面积与矩形ABCD的面积之间的关系.他的思路是:首先过点E作BC的垂线,将其转化为证明三角形全等,然后根据全等三角形的面积相等使问题得到解决.请根据小明的思路完成下面的作图与填空:
证明:用直尺和圆规,过点E作BC的垂线EF,垂足为F(只保留作图痕迹).
在△BAE和△EFB中,
∵EF⊥BC,
∴∠EFB=90°.
又∠A=90°,
∴ ①
∵AD∥BC,
∴ ②
又 ③
∴△BAE≌△EFB(AAS).
同理可得 ④
∴ .
在平面直角坐标系中,抛物线 与 轴相交于点 (点 在点 的左侧),与 轴相交于点 ,连接 .
(1)求点 ,点 的坐标;
(2)如图1,点 在线段 上(点 不与点 重合),点 在 轴负半轴上, ,连接 ,设 的面积为 , 的面积为 , ,当 取最大值时,求 的值;
(3)如图2,抛物线的顶点为 ,连接 ,点 在第一象限的抛物线上, 与 相交于点 ,是否存在点 ,使 ,若存在,请求出点P的坐标;若不存在,请说明理由.
