环保汽车将为2010年上海世博会服务.某辆以蓄电池为驱动能源的环保汽车,总质量m=3×103 kg.当它在水平路面上以v="36" km/h的速度匀速行驶时,驱动电机的输入电流I="50" A,电压U="300" V.在此行驶状态下
(1)求驱动电机的输入功率P电;
(2)若驱动电机能够将输入功率的90%转化为用于牵引汽车前进的机械功率P机,求汽车所受阻力与车重的比值(g取10 m/s2);
(3)设想改用太阳能电池给该车供电,其他条件不变,求所需太阳能电池板的最小面积.结合计算结果,简述你对该设想的思想.
已知太阳辐射的总功率P0=4×1026 W,太阳到地球的距离r=1.5×1011 m,太阳光传播到达地面的过程中大约有30%的能量损耗,该车所用太阳能电池的能量转化效率约为15%.
在图中R1=9Ω,R2=5Ω。当单刀双掷开关S扳到位置“1”时,电压表的示数U1=2.70V;当开关S扳到位置“2”时,电压表的示数U2=2.50V。可得电源的电动势E和内电阻r。
一根长为l的丝线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成370角,重力加速度为g,则这个小球带何种电荷?并求这个匀强电场的电场强度的大小。(已知
 )
)
如图所示,光滑的长平行金属导轨宽度d=50cm,导轨所在的平面与水平面夹角=37°,导轨上端电阻R=0.8,其他电阻不计,导轨放在竖直向上的匀强磁场中,磁感应强度B=0.4T。金属棒ab从上端由静止开始下滑,金属棒ab的质量m=0.1kg。(sin37°=0.6,g=10m/s2)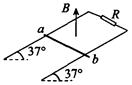
(1)求导体棒下滑的最大速度;
(2)求当速度达到5m/s时导体棒的加速度;
(3)若经过时间t,导体棒下滑的垂直距离为s,速度为v。若在同一时间内,电阻产生的热与一恒定电流I0在该电阻上产生的热相同,求恒定电流I0的表达式(各物理量全部用字母表示)。
一小型发电机通过升压、降压变压器把电能输送给用户,已知发电机的输出功率为为50 kW,输出电压为500 V,升压变压器原、副线圈匝数比为1:5,两个变压器间的输电导线的总电阻为15 Ω,变压器本身的损耗忽略不计,在输电过程中电抗造成电压的损失不计,求:
(1)升压变压器副线圈的端电压;
(2)输电线上损耗的电功率;
如图所示,光滑的金属导轨放在磁感应强度B=0.2T的匀强磁场中。平行导轨的宽度d=0.3m,定值电阻R=0.5。在外力F作用下,导体棒ab以v=20m/s的速度沿着导轨向左匀速运动。导体棒和导轨的电阻不计。求: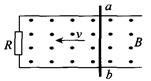
(1)通过R的感应电流大小;
(2)外力F的大小。