我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,
即已知三角形的三边长,求它的面积.用现代式子表示即为: ……①(其中
……①(其中 、
、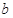 、
、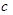 为三角形的三边长,
为三角形的三边长,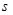 为面积).
为面积).
而另一个文明古国古希腊也有求三角形面积的海伦公式: ……②(其中
……②(其中 ).
).
⑴ 若已知三角形的三边长分别为5、7、8,试分别运用公式①和公式②,计算该三角形的面积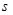 ;
;
⑵ 你能否由公式①推导出公式②?请试试.
已知一次函数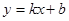 中,当
中,当 时,函数值为
时,函数值为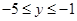 。
。求:这个一次函数的解析式?并画出这个一次函数的图像。
求出这个函数图象与另一个正比例函数
 的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时
的交点坐标,并根据图象写出使一次函数的值大于正比例函数的值时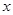 的取值范围。
的取值范围。
在我市某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.乙队单独完成这项工程需要多少天?
甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
阅读理解:对于二次三项式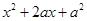 可以直接用公式法分解为
可以直接用公式法分解为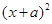 的形式,但对于二次三项式
的形式,但对于二次三项式 ,就不能直接用公式法了,我们可以在二次三项式
,就不能直接用公式法了,我们可以在二次三项式 中先加上一项
中先加上一项 ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 这项,使整个式子的值不变.于是有
这项,使整个式子的值不变.于是有 =
= +
+ -
-
= =
= =
= 。
。
像上面这样把二次三项式分解因式的方法叫做添(拆)项法.请用上述方法求出
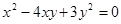 (满足
(满足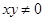 ,且
,且 )中
)中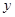 与
与 的关系式。
的关系式。利用上述关系式求
 的值。
的值。
某校需刻录一批电脑光盘,若到电脑公司刻录,每张需8元(包括空白光盘费);若学校自己刻录,除租用刻录机需120元外,每张还需成本4元(包括空白光盘费),问刻录这批光盘到电脑公司刻录费用省,还是自己刻录省?请说明理由。
如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?答:。