如图所示,在四棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
(本小题满分10分)
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
| 时间(将第x天记为x) x |
1 |
10 |
11 |
18 |
| 单价(元/件)P |
9 |
0 |
1 |
8 |
而这20天相应的销售量Q(百件/天)与x对应的点(x,Q)在如图所示的半圆上.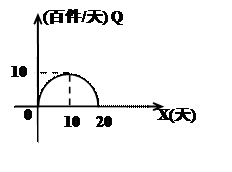
(1)写出每天销售y(元)与时间x(天)的函数关系式y=f(x);
(2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此测试结果应将单价P设定为多少元为好?(结果精确到1元)
(本小题满分12分)
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC, △PAD是等边三角形,已知BD=2AD=8,AB=2DC= (1)设M是PC上的一点,证明:平面MBD⊥平面PAD(2)求四棱锥P-ABCD的体积
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD(2)求四棱锥P-ABCD的体积
(本小题满分12分)
已知数列{an}的前n项和为Sn, Sn+1="4an+2," a1="1," bn=an+1-2an(n∈N*)
(1) 求数列{bn}的前n项和Tn.
(2)求 an
(本小题满分12分)
令函数f(x)= ﹒
﹒ ,
, ="(2cosx,1),"
="(2cosx,1),"  =(cosx,2
=(cosx,2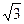 sinxcosx),x∈R
sinxcosx),x∈R
(1)求f(x)的最小正周期与单调增区间
(2)在△ABC中,a,b,c分别是角A,B,C的 对边,已知f(A)=2,b=1,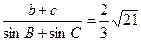 ,求△ABC的面积.
,求△ABC的面积.
椭圆C: 的两个焦点分别为
的两个焦点分别为 ,
,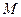 是椭圆上一点,且满足
是椭圆上一点,且满足 。
。
(1)求离心率e的取值范围;
(2)当离心率e取得最小值时,点N( 0 , 3 )到椭圆上的点的最远距离为 。
。
(i)求此时椭圆C的方程;
(ii)设斜率为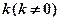 的直线l与椭圆C相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点P(0,
的直线l与椭圆C相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点P(0, )、Q的直线对称?若能,求出
)、Q的直线对称?若能,求出 的取值范围;若不能,请说明理由。
的取值范围;若不能,请说明理由。