用数学归纳法证明“当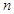 为正奇数时,
为正奇数时,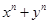 能被
能被 整除”,第二步归纳假设应写成( )
整除”,第二步归纳假设应写成( )
A.假设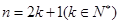 正确,再推 正确,再推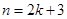 正确; 正确; |
B.假设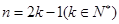 正确,再推 正确,再推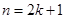 正确; 正确; |
C.假设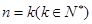 正确,再推 正确,再推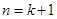 正确; 正确; |
D.假设 正确,再推 正确,再推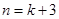 正确。 正确。 |
已知函数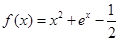
 与
与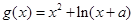 的图象上存在关于y轴对称的点,则a的取值范围()
的图象上存在关于y轴对称的点,则a的取值范围()
A.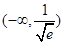 |
B. |
C.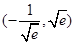 |
D. |
若双曲线
 上存在一点P满足以
上存在一点P满足以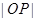 为边长的正方形的面积等于
为边长的正方形的面积等于 (其中O为坐标原点),则双曲线的离心率的取值范围是()
(其中O为坐标原点),则双曲线的离心率的取值范围是()
A. |
B.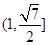 |
C. |
D. |
若关于x的方程 有三个不同的实数解,则实数a的取值范围为()
有三个不同的实数解,则实数a的取值范围为()
A. |
B. |
C. |
D. |
一个几何体的三视图如右图所示,则该几何体的体积是 ()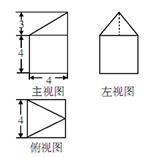
| A.64 | B.72 | C.80 | D.112 |
设a,b,c是空间三条直线, ,
, 是空间两个平面,则下列命题中,逆命题不成立的是()
是空间两个平面,则下列命题中,逆命题不成立的是()
A.当c⊥ 时,若c⊥ 时,若c⊥ ,则 ,则 ∥ ∥ |
B.当 时,若b⊥ 时,若b⊥ ,则 ,则 |
C.当 ,且c是a在 ,且c是a在 内的射影时,若b⊥c,则a⊥b 内的射影时,若b⊥c,则a⊥b |
D.当 ,且 ,且 时,若c∥ 时,若c∥ ,则b∥c ,则b∥c |