2007年5月17日我市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向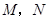 两地之间修建一条道路.已知:如图
两地之间修建一条道路.已知:如图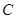 点周围180m范围内为文物保护区,在
点周围180m范围内为文物保护区,在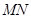 上点
上点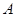 处测得
处测得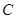 在
在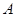 的北偏东
的北偏东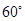 方向上,从
方向上,从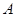 向东走500m到达
向东走500m到达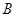 处,测得
处,测得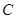 在
在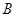 的北偏西
的北偏西 方向上.
方向上.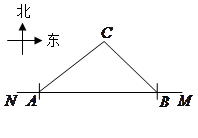
(1)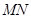 是否穿过文物保护区?为什么?(参考数据:
是否穿过文物保护区?为什么?(参考数据: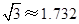 )
)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
如图1:矩形OABC的顶点A、B在抛物线 上,OC在
上,OC在 轴上,且
轴上,且 .
.
(1)求抛物线的解析式及抛物线的对称轴.
(2)如图2,边长为 的正方形ABCD的边CD在
的正方形ABCD的边CD在 轴上,A、B两点在抛物线上,请用含
轴上,A、B两点在抛物线上,请用含 的代数式表示点B的坐标,并求出正方形边长
的代数式表示点B的坐标,并求出正方形边长 的值.
的值.

我市某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y件与售价x元之间存在着如下表所示的一次函数关系.
| 售价x元 |
… |
70 |
90 |
… |
| 销售量y件 |
… |
3000 |
1000 |
… |
(1)求销售量y件与售价x元之间的函数关系式;
(2)设每天获得的利润为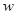 元,当售价x为多少时,每天获得的利润最大?并求出最大值.
元,当售价x为多少时,每天获得的利润最大?并求出最大值.
不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为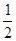 .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心 ,另一边所在直线与半圆相交于点
,另一边所在直线与半圆相交于点 ,量出半径
,量出半径 ,弦
,弦 ,求这把直尺的宽度.
,求这把直尺的宽度.
如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
(1)求∠D的度数;
(2)求证:AC2=AD·CE.