某校300名优秀学生，中考数学得分范围是70—119(得分都是整数)，为了了解该校这300名学生的中考数学成绩，从中抽查了一部分学生的数学分数，通过数据处理，得到如下频率分布表和频率分布直方图.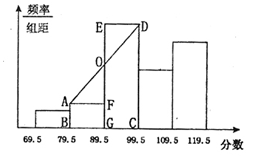
| 分组 |
频数 |
频率 |
| 109.5—119.5 |
15 |
0.30 |
| 99.5--109.5 |
10 |
0.20 |
| 89.5—99.5 |
18 |
|
| 79.5—89.5 |
|
|
| 69.5—79.5 |
3 |
0.06 |
| 合计 |
|
1.00 |
请你根据给出的图标解答：
(1)填写频率分布表中未完成部分的数据；
(2)指出在这个问题中的总体和样本容量；
(3)求出在频率分布直方图中直角梯形ABCD的面积；
(4)请你用
，可以得到哪些信息？(写一条即可)
（巴中）如图，在平面直角坐标系xOy中，二次函数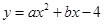
（
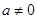）的图象与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．
（1）求该二次函数的解析式；
（2）如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；
（3）如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．
（广安）如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．
（1）求证：PA是⊙O的切线；
（2）若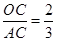
，且OC=4，求PA的长和tanD的值．
（广安）如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：
经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线
顶点E在直线l上．
（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；
（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；
（3）设抛物线与y轴交于G点，当抛物线顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．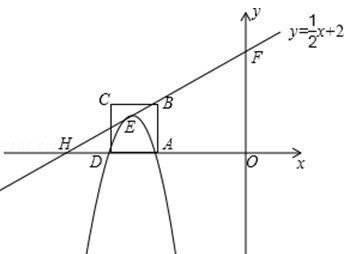
（广元）经统计分析．某市跨河大桥上的车流速度v（千米／时）是车流密度x（辆／千米）的函数，当桥上的车流密度达到220辆／千米的时候就造成交通堵塞．此时车流速度为0千米／时；当车流密度不超过20辆／千米，车流速度为80千米／时．研究表明：当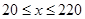
时，车流速度v是车流密度x的一次函数．
（1）求大桥上车流密度为100辆／千米时的车流速度；
（2）在某一交通时段．为使大桥上的车流速度大于60千米／时且小于80千米／时，应把大桥上的车流密度控制在什么范围内？
（广元）如图，AB是⊙O的弦，D为半径OA的中点．过D作CD⊥OA交弦AB于点E，交⊙O于点F．且CE=CB．
（1）求证：BC是⊙O的切线；
（2）连接AF、BF，求∠ABF的度数；
（3）如果CD=15，BE=10，sinA=
．求⊙O的半径．