北京时间2009年3月1日下午15时36分,在距月球表面100 km的圆轨道上运行的质量为1.2×103 kg(连同燃料)的“嫦娥一号”卫星,在北京航天飞行控制中心科技人员的控制下发动机点火,在极短的时间内以4.92 km/s的速度(相对月球表面)向前喷出质量为50 kg的气体后,卫星减速,只在月球引力的作用下下落,最后成功撞击到月球东经52.36度、南纬1.50度的预定的丰富海区域,实现了预期目标,为中国探月一期工程画上一个圆满的句号.已知月球的半径R="1.7×103" km,月球表面的重力加速度g′=1.8 m/s2,
求:(1)“嫦娥一号”在圆轨道上的运行速度;
(2)若忽略卫星下落过程中重力加速度的变化,求“嫦娥一号”撞击到月球表面时的速度.
如图所示,上端开口的光滑圆形气缸竖直放置,活塞将一定质量的气体封闭在气缸内。在气缸内距缸底60cm处设有卡环ab,使活塞只能向上滑动。开始时活塞搁在ab上,缸体内气体的压强等于大气压强为p0,活塞因重力而产生的压强为0.2p0,气体起始温度为300K,现缓慢加热气缸内气体,求: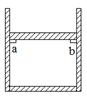
(1)温度为多少时活塞开始离开ab?
(2)当温度缓慢升为多少时,活塞活塞离缸底80cm?
如图所示的装置是在竖直平面内放置光滑的绝缘轨道,处于水平向右的匀强电场中,一带负电荷的小球从高h的A处静止开始下滑,沿轨道ABC运动后进入圆环内作圆周运动.已知小球所受到电场力是其重力的3/4,圆环半径为R,斜面倾角为θ=53°,SBC=2R.若使小球在圆环内能作完整的圆周运动,h至少为多少?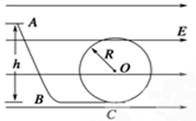
高速连续曝光照相机可在底片上重叠形成多个图象.现利用这架照相机对MD-2000家用汽车的加速性能进行研究,如下图所示为汽车做匀加速直线运动时三次曝光的照片,图中的标尺单位为米,照相机每两次曝光的时间间隔为1.0 s.已知该汽车的质量为2000 kg,额定功率为72 kW,汽车运动过程中所受的阻力始终为1600 N.
(1)求该汽车的加速度.
(2)若汽车由静止以此加速度开始做匀加速直线运动,匀加速运动状态最多能保持多长时间?
(3)求汽车所能达到的最大速度.
如下图所示,一个质量为m=0.6 kg的小球,以某一初速度v0从图中P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧轨道(不计空气阻力,进入时无机械能损失).已知圆弧半径R=0.3 m,图中θ=60°,小球到达A点时的速度v=4 m/s.(取g=10 m/s2)试求:
(1)小球做平抛运动的初速度v0.
(2)判断小球能否通过圆弧最高点C,若能,求出小球到达圆弧轨道最高点C时对轨道的压力FN.
如图九所示,轻绳悬挂一质量为m=2.0kg的小球,现对小球再施加一个力F,使小球静止在绳子与竖直方向成60º的位置上,g取10m/s2。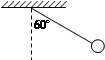
(1)若F为水平方向,求F的大小;
(2)若要使F的取值最小,求F的大小和方向。