(20分)如图所示,轻弹簧一端连于固定点O,可在竖直平面内自由转动,另一端连接一带电小球P,其质量m=2×10-2 kg,电荷量q="0.2" C.将弹簧拉至水平后,以初速度V0="20" m/s竖直向下射出小球P,小球P到达O点的正下方O1点时速度恰好水平,其大小V="15" m/s.若O、O1相距R="1.5" m,小球P在O1点与另一由细绳悬挂的、不带电的、质量M=1.6×10-1 kg的静止绝缘小球N相碰。碰后瞬间,小球P脱离弹簧,小球N脱离细绳,同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=1T的弱强磁场。此后,小球P在竖直平面内做半径r="0.5" m的圆周运动。小球P、N均可视为质点,小球P的电荷量保持不变,不计空气阻力,取g="10" m/s2。那么,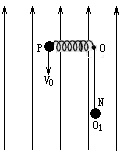
(1)弹簧从水平摆至竖直位置的过程中,其弹力做功为多少?
(2)请通过计算并比较相关物理量,判断小球P、N碰撞后能否在某一时刻具有相同的速度。
(3)若题中各量为变量,在保证小球P、N碰撞后某一时刻具有相同速度的前提下,请推导出r的表达式(要求用B、q、m、θ表示,其中θ为小球N的运动速度与水平方向的夹角)。
铜的摩尔质量为6.4×10–2 kg/mol,密度为8.9×10 3 kg/m3,阿伏加德罗常数为6.0×1023 mol-1若每个铜原子提供一个自由电子,则铜导体中自由电子的密度为 m-3.(保留两位有效数字)
绳系着装水的水桶,在竖直平面内做圆周运动,水的质量m = 0.5kg,绳长L = 40cm,求:
(1)为使桶在最高点时水不流出,桶的最小速率?
(2)桶在最高点速率v = 3m/s时,水对桶底的压力?
长为L的细线,拴一质量为m的小球,一端固定于O点。让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示,当摆线L与竖直方向的夹角是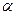 时,求:
时,求:
(1)线的拉力F;
(2)小球运动的线速度的大小;
(3)小球运动的角速度及周期
许多仪器中可利用磁场控制带电粒子的运动轨迹。如图所示的真空环境中,有一半径r="0.05" m的圆形区域内存在磁感应强度B="0.2" T的匀强磁场,其右侧相距d=0.05m处有一足够大的竖直屏。从S处不断有比荷 =1×108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上。不计粒子重力,求:
=1×108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上。不计粒子重力,求: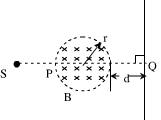
(1)粒子在磁场中做圆周运动的轨迹半径;
(2)绕通过P点(P点为SQ与磁场边界圆的交点)垂直纸面的轴,将该圆形磁场区域逆时针缓慢转动90°的过程中,粒子在屏上能打到的范围。
学校有一台应急备用发电机,内阻为r= 1Ω,升压变压器匝数比为1∶6,降压变压器的匝数比为6∶1,输电线的总电阻为R=4.5Ω,全校22个教室,每个教室用“220V,40W”的灯6盏,要求所有灯都正常发光,变压器均
1Ω,升压变压器匝数比为1∶6,降压变压器的匝数比为6∶1,输电线的总电阻为R=4.5Ω,全校22个教室,每个教室用“220V,40W”的灯6盏,要求所有灯都正常发光,变压器均 为理想变压器,求:
为理想变压器,求:
(1)输电线上损耗的电功率多大?
(2)发电机的电动势多大?