如图所示是上海“明珠线”某车站的设计方案.由于站台建得稍高,电车进站时要上坡,出站时要下坡.忽略斜坡的摩擦力,你能分析这种设计的优点吗?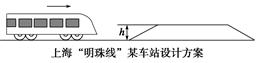
如图所示,一根重8N的均匀直棒AB,A端用细绳吊在固定点O上,现用一水平方向6N的力作用于棒的B端。试求绳跟竖直方向成多大角度时才平衡?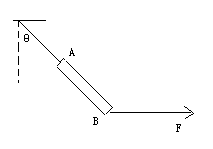
一人通过箱带拉着一个旅行箱前进,拉力是12 N,箱带与水平面夹角是30°,则拉力的水平分力是多大?竖直分力是多大?
如图7所示,物块和斜面体的质量分别为m.M,物块在平行于斜面的推力F作用下沿斜面加速度a向上滑动时,斜面体仍保持静止.斜面倾角为θ,试求地面对斜面体的支持力和摩擦力.
如图6所示,静止在水平面上的纸带上放一质量m为的小金属块(可视为质点), 金属块离纸带右端距离为L, 金属块与纸带间动摩擦因数为μ.现用力向左将纸带从金属块下水平抽出,设纸带加速过程极短,可认为纸带在抽动过程中一直做匀速运动.求:
(1)属块刚开始运动时受到的摩擦力的大小和方向;
(2)要将纸带从金属块下水平抽出,纸带的速度v应满足的条件.
质量m=1.5Kg的物块(可视为质点)在水平恒力F的作用下,从水平面上A点由静止开始运动,运动一段距离撤去该力,物体继续滑行t=2.0s停在B点.已知AB两点间的距离S=5.0m,物块与水平面间的动摩擦因数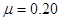 ,求恒力F为多大?(g=10m/s2)
,求恒力F为多大?(g=10m/s2)