已知 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中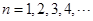
(1)证明:数列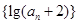 是等比数列;
是等比数列;
(2)设数列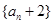 的前
的前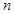 项积为
项积为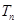 ,求
,求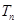 及数列
及数列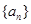 的通项公式;
的通项公式;
(3)已知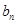 是
是 与
与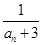 的等差中项,数列
的等差中项,数列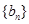 的前
的前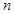 项和为
项和为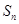 ,求证:
,求证: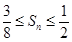 .
.
(1)写出点P(1,3,-5)关于原点成中心对称的点的坐标;
(2)写出点P(1,3,-5)关于ox轴对称的点的坐标。
(1)写出点P(2,3,4)在三个坐标平面内的射影的坐标;
(2)写出点P(2,3,4)在三条坐标轴上的射影的坐标。
在空间直角坐标系中,落在x轴上和xoy坐标平面内的点的坐标各有什么特点?试分别写出三个落在x轴和xoy平面内的点的坐标(答案不唯一)。
如图,已知正方体 的棱长为a,M为
的棱长为a,M为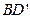 的中点,点N在
的中点,点N在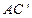 上,且
上,且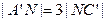 ,试求MN的长.
,试求MN的长.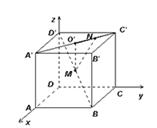
如图,在四棱锥P-ABCD中,底面ABCD为正方形,且边长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G,H,写出点E,F,G,H的坐标.