某储蓄所去年储户存款为2300万元,今年与去年相比,定期存款增加了25﹪,而活期存款减少了25﹪,但存款总额增加了15﹪,问今年的定期、活期存款各是多少?
有一个两位数,个位数字与十位数字之和为10,若将个位数字与十位数字互换,则所得新数比原数小18,求这个两位数?
今年“五一”黄金周期间,河池市某旅行社接待一日游和三日游的旅客共1600人,收取旅游费129万元,其中一日游每人收费150元,三日游每人收费1200元. 该旅行社接待的一日游和三日游旅客各多少人?
《一千零一夜》中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在树下觅食,树上的一只鸽子对树下觅食的鸽子说:“若从你们中飞上来一只,则树下的鸽子就是整个个群的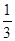 ;若从树上飞下去一只,则树上、树下的鸽子就一样多拉。”你知道树上、树下各有多少只鸽子吗?
;若从树上飞下去一只,则树上、树下的鸽子就一样多拉。”你知道树上、树下各有多少只鸽子吗?
一个车间加工轴杆和轴承,每人每天可以加工轴杆12根,或者轴承15个,车间共90人,应该怎样调配人力,才能使每天生产的轴杆和轴承正好相等?