某校师生积极为某地震灾区捐款,在得知灾区急需帐蓬后,立即到当地的一家帐蓬厂采购,帐蓬有两种规格:可供3人居住的小组帐蓬,价格为每顶160元;可供10人居住的大帐蓬,价格为每顶400元.学校共花去捐款96000元,正好可供2300人临时居住.
(1)求该校采购了多少顶3人小帐蓬?多少顶10人大帐蓬?
(2)学校计划租用甲、乙两种型号的卡车共20辆,把这批帐篷紧急运往灾区,已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷 和7顶大帐篷,应如何安排甲、乙两种型号卡车可一次将这批帐篷运往灾区?有哪几种租车方案?
如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC,垂足为M。求证:M是BE的中点。
某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降。今年1开始A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元。今年1月份A款汽车每辆售价多少万元?
若△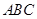 的三边
的三边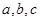 满足
满足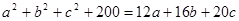 ,试判断△
,试判断△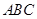 的形状.
的形状.
已知 =
= ,试说明不论x为任何有意义的值,y的值均不变.
,试说明不论x为任何有意义的值,y的值均不变.
从2004年8月1日起,浙江省城乡居民生活用电执行新的电价政策:安装“一户一表”的居民用户,按所抄见电量(每家用户电表所表示的用电量)实行阶梯式累进加价,收费标准如下:
例:若某户月用电300千瓦时,需交电费为 (元)
(元)
(1)若10月份王老师家用电量为120千瓦时,则10月份王老师家应付电费多少元?
(2)已知王老师家10月份的用电量为a 千瓦时,请完成下列填空:
①若a≤50 千瓦时,则10月份王老师家应付电费为_____________ 元;
②若50<a≤200 千瓦时,则10月份王老师家应付电费为_____________元;
③若a>200 千瓦时,则10月份王老师家应付电费为_____________元.
(3)若10月份王老师家应付电费为96.50元,则10月份王老师家的用电量是多少千瓦时?