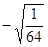 的立方根是 .
的立方根是 .
如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若四边形ABED的面积等于8,则平移距离等于()
| A.2 | B.4 | C.8 | D.16 |
如图,已知∠EFD=∠BCA,BC=EF,AF=DC.若将△ABC沿AD向右平移,使点C与点D重合,则所得到的图形形状是()
A.梯形 B.平行四边形 C.矩形 D.等边三角形
如图,直线m∥n,圆心在直线n上的⊙A是由⊙B平移得到的,则图中两个阴影三角形的面积大小关系是()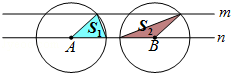
| A.S1<S2 | B.S1=S2 | C.S1<S2 | D.不能确定 |
如图,将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD的周长为()
| A.12 | B.16 | C.20 | D.24 |
在图示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是()
A. |
B. |
C. |
D. |