命题“所有偶数的立方是偶数”的否定是 。
若定义在R上的函数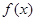 满足
满足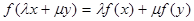 ,
,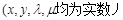 ,则称
,则称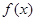 为R上的线性变换,现有下列命题:
为R上的线性变换,现有下列命题:
①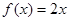 是R上的线性变换
是R上的线性变换
②若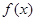 是R上的线性变换,则
是R上的线性变换,则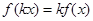
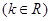
③若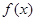 与
与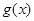 均为R上的线性变换,则
均为R上的线性变换,则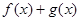 是R上的线性变换
是R上的线性变换
④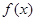 是R上的线性变换的充要条件为
是R上的线性变换的充要条件为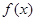 是R上的一次函数
是R上的一次函数
其中是真命题有(写出所有真命题的编号)
设过点 的直线
的直线 分别与
分别与 正半轴,
正半轴,  轴正半轴交于
轴正半轴交于 两点,
两点, 为坐标原点,则三角形
为坐标原点,则三角形 面积最小时直线方程为
面积最小时直线方程为
已知数列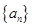 的首项
的首项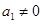 ,其前
,其前 项的和为
项的和为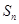 ,且
,且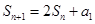 ,则
,则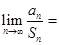 ____
____
已知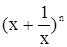 的展开式中所有项的二项式系数和为64,则展开式的常数项是_________.
的展开式中所有项的二项式系数和为64,则展开式的常数项是_________.
给出下列四个命题
(1)函数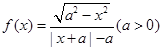 ,既不是奇函数,又不是偶函数;
,既不是奇函数,又不是偶函数;
(2) 且
且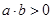 ,则函数
,则函数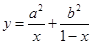 的最小值是
的最小值是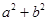 ;
;
(3)已知向量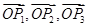 满足条件
满足条件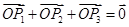 ,且
,且 ,则
,则 为正三角形;
为正三角形;
(4)已知 ,若不等式
,若不等式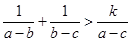 恒成立,则
恒成立,则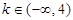 ;
;
其中正确命题的有_ _____(填出满足条件的所有序号)