如图正方形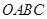 的面积为4,点
的面积为4,点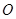 为坐标原点,点
为坐标原点,点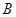 在函数
在函数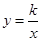 (
(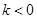 ,
,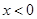 )的图象上,点
)的图象上,点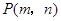 是函数
是函数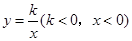 的图象上异于
的图象上异于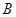 的任意一点,过点
的任意一点,过点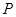 分别作
分别作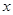 轴,
轴,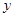 轴的垂线,垂足分别为
轴的垂线,垂足分别为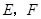 .
.
(1)设矩形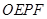 的面积为
的面积为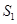 ,判断
,判断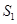 与点
与点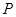 的位置是否有关(不必说理由).
的位置是否有关(不必说理由).
(2)从矩形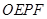 的面积中减去其与正方形
的面积中减去其与正方形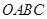 重合的面积,剩余面积记为
重合的面积,剩余面积记为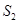 ,写出
,写出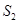 与
与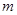 的函数关系,并标明
的函数关系,并标明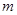 的取值范围.
的取值范围.
为体现社会对教师的尊重,教师节这天上午,出租车司机小王在东西走向的公路上免费接送老师。如果规定向东为正,向西为负,出租车的行程如下。(单位:千米)
+15-4+13-10-12+3-13-17 当最后一名老师到达目的地时,小王距离开始接送第一位老师之前的地点的距离是多少?
若出租车的耗油量为0.4升/千米,这天上午出租车共耗油多少升?
已知长方形的生活小区OBCD的边长分别为40米和130米,如图,建立平面直角坐标系,“创文明城市”宣传车点P从点o出发,沿OB运动至点B停止,宣传车点Q从点C出发,沿CD运动至点D停止,两车同时出发,速度都是1米/秒;宣传车音响半径可达25米,
(两点间距离公式: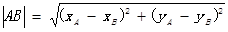 )
)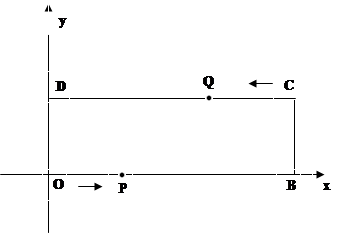
求直线OC的解析式
几秒时,
 为等腰三角形?
为等腰三角形?两辆宣传车的声音是否会互相干扰?如果会,求出受干扰的时间多长;如果不会干扰,写出理由。
福州市某楼盘准备以每平方米10000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米8100元的均价开盘销售求平均每次下调的百分率
某人准备以开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.9折销售;②不打折,送两年物业管理费.物业管理费是每平方米每月1元.请问哪种方案更优惠?
在直径为100cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=80cm,求油的最大深度。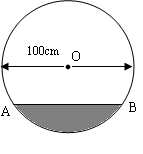
如图,在网格中有一个四边形的图案。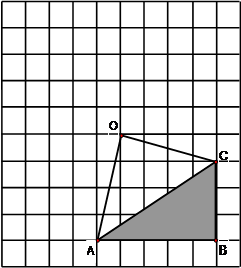
请你画出此图案绕点O顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
若网格中每个小正方形的边长为1,旋转后点
 的对应点依次为
的对应点依次为 ,
,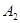 ,
,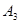 ,求四边形
,求四边形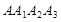 的面积;
的面积;这个美丽图案能够证明一个我们学过的著名定理,请直接写出这个定理名称,不要求证明。