如图,在梯形纸片ABCD中,BC∥AD,∠A+∠D=90°,tanA=2,过点B作BH⊥AD与H,BC=BH=2.动点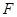 从点
从点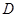 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿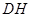 运动到点
运动到点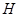 停止,在运动过程中,过点
停止,在运动过程中,过点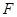 作
作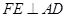 交折线
交折线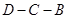 于点
于点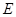 ,将纸片沿直线
,将纸片沿直线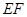 折叠,点
折叠,点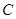 、
、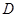 的对应点分别是点
的对应点分别是点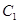 、
、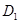 。设
。设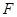 点运动的时间是
点运动的时间是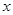 秒(
秒(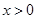 )。
)。
(1)当点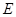 和点
和点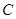 重合时,求运动时间
重合时,求运动时间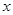 的值;
的值;
(2)在整个运动过程中,设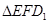 或四边形
或四边形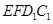 与梯形
与梯形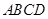 重叠部分面积为
重叠部分面积为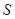 ,请直接写出
,请直接写出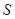 与
与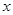 之间的函数关系式和相应自变量
之间的函数关系式和相应自变量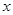 的取值范围;
的取值范围;
(3)平移线段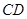 ,交线段
,交线段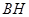 于点
于点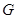 ,交线段
,交线段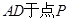 。在直线
。在直线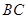 上存在点
上存在点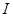 ,使
,使 为等腰直角三角形。请求出线段
为等腰直角三角形。请求出线段 的所有可能的长度。
的所有可能的长度。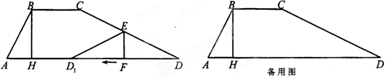
如图,在菱形 中, , ,连接 .
(1)求 的长;
(2)点E为线段 上一动点(不与点B,D重合),点 在边 上,且 .
①当 时,求四边形 的面积;
②当四边形 的面积取得最小值时, 的值是否也最小?如果是,求 的最小值;如果不是,请说明理由.

已知直线 经过点 和点 .
(1)求直线 的解析式;
(2)若点 在直线l上,以P为顶点的抛物线G过点 ,且开口向下.
①求m的取值范围;
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单位长度后得到的点 也在G上时,求G在 的图象的最高点的坐标.
某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE, .
(1)求 的长;
(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.
条件①: ;条件②:从D处看旗杆顶部A的仰角 为 .
注:如果选择条件①和条件②分别作答,按第一个解答计分.
参考数据: .

如图,AB是⊙O的直径,点C在⊙O上,且 .
(1)尺规作图:过点O作AC的垂线,交劣弧 于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求点O到AC的距离及 的值.

已知 .
(1)化简 ;
(2)若关于 的方程 有两个相等的实数根,求 的值.