“回归”一词是在研究子女的身高与父母的身高之间的遗传关系时,由高尔顿提出的,他的研究结果是子代的平均身高向中心回归,根据他的结论,在儿子的身高y与父亲的身高x的回归方程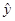 =a+bx中,b的取值
=a+bx中,b的取值
| A.在(-1,0)内 | B.等于0 | C.在(0,1)内 | D.在[1,+∞)内 |
如果直线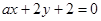 与直线
与直线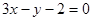 平行,则系数
平行,则系数 ( )
( )
A.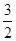 |
B.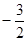 |
C.-3 | D.-6 |
圆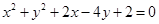 的圆心坐标和半径分别为 ( )
的圆心坐标和半径分别为 ( )
A.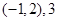 |
B.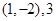 |
C.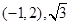 |
D.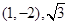 |
已知定义在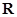 上的奇函数
上的奇函数 满足
满足 ,且
,且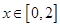 时,
时,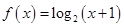 ,甲,乙,丙,丁四位同学有下列结论:甲:
,甲,乙,丙,丁四位同学有下列结论:甲: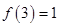 ;乙:函数
;乙:函数 在
在 上是增函数;丙:函数
上是增函数;丙:函数 关于直线
关于直线 对称;丁:若
对称;丁:若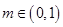 ,则关于
,则关于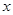 的方程
的方程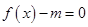 在
在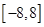 上所有根之和为-8,其中正确的是()
上所有根之和为-8,其中正确的是()
| A.甲,乙,丁 | B.乙,丙 | C.甲,乙,丙 | D.甲,丁 |
已知 , (
, ( >0 ,
>0 ,  ) , A、B为图象上两点,B是图象的最高点,C为B在x轴上的射影,且点C的坐标为
) , A、B为图象上两点,B是图象的最高点,C为B在x轴上的射影,且点C的坐标为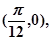 则
则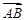 ·
· ( ).
( ).
A. 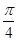
 B.
B. 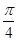
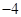 C. 4 D.
C. 4 D. 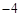
已知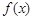 ,
, 都是定义在
都是定义在 上的函数,且满足以下条件:
上的函数,且满足以下条件:
①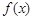 =
=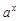 ·
· (
( );②
);②
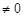 ; ③
; ③ ;
;
若 ,则
,则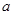 等于( )
等于( )
A. |
B.2 | C.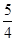 |
D.2或 |