为发展旅游经济.我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人.非节假日打a折售票.节假日按团队人数分段定价售票,即m人以下(含m人)的团队接原价售票;超过m人的团队.其中m人仍按原价售票.超过m人部分的游客打b折售票.设某旅游团人数为x人.非节假日购票款为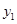 (元),节假日购票款为
(元),节假日购票款为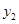 (元).
(元).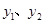 与x之间的函数图象如图所示.
与x之间的函数图象如图所示.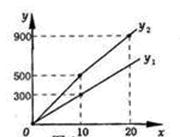
(1)观察图象可知:a=______;b=______;m=______;
(2)直接写出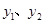 与x之间的函数关系式:
与x之间的函数关系式:
(3)某旅行导游王娜于5月1日带A团.5月20日(非节假日)带B团都到该景区旅游.共付门票款1900元.A, B两个团队合计50人,求A,B两个团队各有多少人?
(梧州)如图,抛物线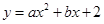 与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
(1)求此抛物线的解析式;
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标;
(3)过D点作直线DH∥AC交AB于H,当△DHF的面积最大时,在抛物线和直线AB上分别取M、N两点,并使D、H、M、N四点组成平行四边形,请你直接写出符合要求的M、N两点的横坐标.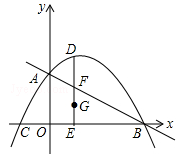
(梧州)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.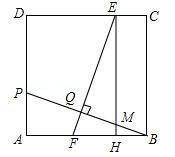
(梧州)梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A、B两种品牌的龟苓膏共1000包.
(1)若小王按需购买A、B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式.
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本(运算结果取整数)?
(钦州)如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.
(1)用含t的式子表示点E的坐标为_______;
(2)当t为何值时,∠OCD=180°?
(3)当点C与点F不重合时,设△OCF的面积为S,求S与t之间的函数解析式.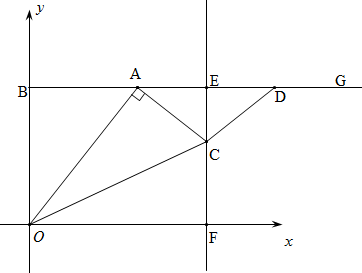
(柳州)如图,已知抛物线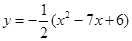 的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式: (
( ),并指出顶点M的坐标;
),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.