为了了解全善学校初一、初二年级1500名学生对学校设置的象棋、体操，篮球、合唱、跑步等课外活动的喜爱情况，在初一初二的学生中随机抽取了若干名学生，对他们喜爱的课外活动（每人只选一项）进行了问卷调查，将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图（均不完整）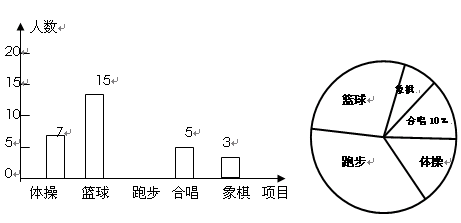
（1）在这次问卷调查中，一共抽查了 名学生；
（2）补全频数分布直方图；
（3）估计两个年级的1500名学生中有 人喜爱篮球运动。
（4）若被随机调查的学生中喜欢合唱的有3名女生，被随机调查的学生中喜欢象棋的有2名男生。现要从随机调查的学生中喜欢合唱的同学和随机调查的学生中喜欢象棋的同学中分别选出一位参加该学校组织的课外活动总结会，请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率。
证明题：说明理由(7分)如图，已知BE⊥
AC于E，CF⊥AB于F，BE、CF相交于点D，若BD=CD.求证：AD平分∠BAC.
证明：∵BE⊥AC于E，CF⊥AB于F
∴∠BFD=∠CED=90°
又∵∠BDF=∠CDE( ) BD=CD
∴△BDF≌△CDE( )
∴DF=DE( )
∴AD平分∠BAC( ).
解方程：(8分)
(1)2x2-4x-5=0 (2)(x-2)2=(2x+3)2
作图题(5分)
已知：∠ABC和线段
DE，求作一点P，使这一点到∠ABC两边的距离相等并且到线段DE两端点的距离也相等.(不要求写作法，保留作图痕迹)
(1)如图1，在正方形AB
CD中，点E、F分别在边BC，CD上，AE，BF交于点O，∠AOF=90°.求证：BE=CF.
(2)如图2，在正方形ABCD中，点E，H，F，G分别在边AB，BC，CD，DA上，EF，GH交于点O，∠FOH=90°，EF=4.求GH的长.
(3)已知点E，H，F，G分别在矩形ABCD的边AB，BC，CD，DA上，EF，GH交于点O，∠FOH=90°，EF=4.直接写出下列两题的答案：
①如图3，矩形ABCD由2个全等的正方形组成，GH=____.
②如图4，矩形ABCD由n个全等的正方形组成，GH=____(用含n的代数式表示)
列方程解应用题(10分)
某
单位组织职工旅游.下面是领队向旅行社导游咨询收费标准的一段对话：
领队：组团去“医巫闾山”旅游每人收费是多少？
导游：如果人数不超过25人，人均旅游费用为100元.
领队：超过25人怎样优惠呢？
导游：如果超过25人，每增加1人，人均旅游费用降低2元，但人均旅游费用不得低于70元.
该单位按旅行社的收费标准组团游览“医巫闾山”结束后，共支付给旅行社 2700元.
请你根据上述信息，求该单位这次到“医巫闾山”旅游的共有多少人？