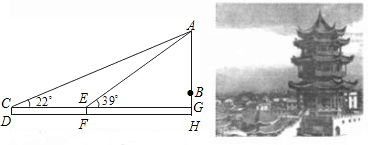
极具特色的“八卦楼”(又称“威镇阁”)是漳州的标志性建筑,它建立在一座平台上.为了测量“八卦楼”的高度AB,小华在D处用高1.1米的测角仪CD,测得楼的顶端A的仰角为22o;再向前走63米到达F处,又测得楼的顶端A的仰角为39o(如图是他设计的平面示意图).已知平台的高度BH约为13米,请你求出“八卦楼”的高度约多少米?
(参考数据:sin22o≈ ,tan220≈
,tan220≈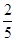 ,sin39o≈
,sin39o≈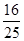 ,tan39o≈
,tan39o≈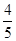 )
) 
已知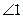 、线段AB及射线OM,按下列要求画图:
、线段AB及射线OM,按下列要求画图: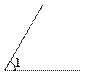


(1)在射线OM上取一点C,使OC=AB;
(2)画 ;
;
(3)在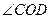 的边OD上取一点E,使OE=2AB;
的边OD上取一点E,使OE=2AB;
(4)测量点E与点C之间的距离为 cm(精确到1cm).
(每小题5分,共10分)
计算:
(1)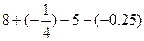 ;
;
(2)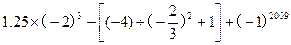 .
.
已知数轴上两点A、B对应的数分别为-1、3, 点P是数轴上一动点P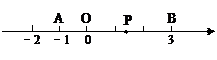
(1)(4分)若点P到点A,点B的距离相等,求点P对应的数;
(2) (6分)当点P以每分钟5个单位长度的速度从O点向右运动时,点A以每分钟3个单位长度的速度向右运动,点B以每分钟2个单位长度的速度向右运动,问几分钟时点P到点A,点B的距离相等.
永川区某中学为了营造良好的文化氛围,学校决定在学校的一段文化墙上制作一幅永久性的标语,为此,在文化墙上特别做了一个长1640cm的长方形横标框,铺红色衬底.为了使制作时方便、制作出来的标语美观,对有关数据作了如下规定:边空:字宽:字距=6:9:2,如图所示.
根据这个规定,若这幅标语名称的字数为14,则边空、字宽、字距各是多少?
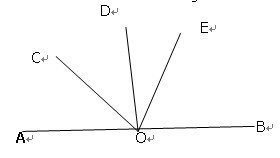
如图,AB为直线,OC是∠AOD的平分线,OE在∠BOD内,DOE=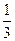 ∠BOD,
∠BOD,
∠COE=72°,求∠EOB