小丁将中国的清华大学、北京大学及英国的剑桥大学的图片分别贴在3张完全相同的不透明的硬纸板上,制成名校卡片,如图.小丁将这3张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,放回后洗匀,再随机抽取一张卡片.
(1) 小丁第一次抽取的卡片上的图片是剑桥大学的概率是多少?(请直接写出结果)
(2) 请你用列表法或画树状图(树形图) 法,帮助小丁求出两次抽取的卡片上的图片一个是国内大学、一个是国外大学的概率.(卡片名称可用字母表示)
分解因式(1)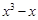
(2)-2x+x2+1
计算或化简(1)(—3)0+(+0.2)2009×(+5)2010
(2)2(x+4) (x-4)
如图,方格纸中的△ABC的三个顶点分别在小正方形的顶点(格点)上,称为格点三角形.请在方格纸上按下列要求画图.
在图①中画出与△ABC全等且有一个公共顶点的格点△ ;
;
在图②中画出与△ABC全等且有一条公共边的格点△ .
.
上海世博会会期为2010年5月1日至2010年10月31日。门票设个人票和团队票两大类。个人普通票160元/张,学生优惠票100元/张;成人团队票120元/张,学生团队票50元/张。
(1)如果2名老师、10名学生均购买个人票去参观世博会,请问一共要花多少元钱购买门票?
(2)用方程组解决下列问题:如果某校共30名师生去参观世博会,并得知他们都是以团队形式购买门票,累计花去2200元,请问该校本次分别有多少名老师、多少名学生参观世博会?
小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
(1)请将表格补充完整;
(2)请将条形统计图补充完整.
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?