如图,在真空中,半径为R的虚线所围的圆形区域内存在匀强磁场,磁场方向垂直纸面向外。在磁场右侧有一对平行金属板M和N,两板间距离也为R,板长为2R,两板的中心线O1O2与磁场区域的圆心O在同一直线上,两板左端与O1也在同一直线上。现有一电荷量为q、质量为m的带正电粒子,以速率v0从圆周上的最低点P沿垂直于半径OO1并指向圆心O的方向进人磁场,当从圆周上的O1点飞出磁场时,给M、N板加上如右边图所示电压u,最后粒子刚好以平行于N板的速度从N板的边缘飞出,不计平行金属板两端的边缘效应及粒子所受的重力,
(1)求磁场的磁感应强度B的大小;
(2)求交变电压的周期T和电压U0的值;
(3)若t= 时,将该粒子从MN板右侧沿板的中心线O2O1,仍以速率v0射人M、N之间,求粒子从磁场中射出的点到P点的距离.
时,将该粒子从MN板右侧沿板的中心线O2O1,仍以速率v0射人M、N之间,求粒子从磁场中射出的点到P点的距离.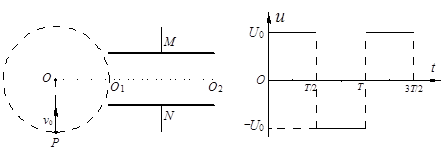
机械横波某时刻的波形图如图所示,波沿x轴正方向传播,质点p的坐标x=0.32m.从此
时刻开始计时.问: 
①若每间隔最小时间0.4 s重复出现波形图.求波速?
②若p点经0.4 s到达平衡位置.求波速?
如图所示,光滑导轨MN、PQ在同一水平面内平行固定放置,其间距d=1 m,右端通过导线与阻值RL=8 Ω的小灯泡L相连,CDEF矩形区域内有方向竖直向下、磁感应强度B=1 T的匀强磁场,一质量m=50 g、阻值为R=2 Ω的金属棒在恒力F作用下从静止开始运动s=2 m后进入磁场恰好做匀速直线运动.(不考虑导轨的电阻,金属棒始终与导轨垂直并保持良好接触).求: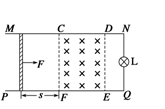
(1)恒力F的大小;
(2)小灯泡发光时的电功率.
单色细光束射到折射率n=  的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).
的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).
(1)在图上大致画出光线在球内的路径和方向;
(2)求入射光线与出射光线之间的夹角α;
如图所示为一简谐波某时刻的波形图,已知该时刻P质点的振动方向向下,波速为2.4m/s,那么再经过t=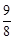 s时,
s时,
(1)B点相对于平衡位置的位移为多少?通过的路
程为多少?
(2)这列波继续向前传播了多大距离?
如图所示的变压器的原线圈1接到220 V的交流电源上.副线圈2的匝数n2=30匝,与一个“11 V, 11 W”的灯泡L连接,L能正常发光.副线圈3的输出电压U3=110 V,与电阻R连接,通过R的电流为0.4 A,求:
(1)副线圈3的匝数n3 .
(2)原线圈1的匝数n1和电流I1.