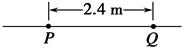一个质量为1500 kg行星探测器从某行星表面竖直升空,发射时发动机推力恒定,发射升空后8 s末,发动机突然间发生故障而关闭;如图19所示为探测器从发射到落回出发点全过程的速度图象;已知该行星表面没有大气,不考虑探测器总质量的变化;求:
(1)探测器在行星表面上升达到的最大高度;
(2)探测器落回出发点时的速度;
(3)探测器发动机正常工作时的推力。
如图所示,LC电路中C是带有电荷的平行板电容器,两极板水平放置.开关S断开时,极板间灰尘恰好静止.当开关S闭合时,灰尘在电容器内运动.若C=0.4 μF,L=1 mH,求: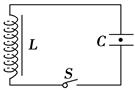
(1)从S闭合开始计时,经2π×10-5 s时,电容器内灰尘的加速度大小为多少?
(2)当灰尘的加速度多大时,线圈中电流最大?
一雷达向一方向发射不连续的无线电波,每次发射的时间为百万分之一秒,两次发射的时间间隔是万分之一秒.图是雷达指示器的显示屏上显示的情景,P为发射出去的无线电波的某一尖形波,Q为其遇到障碍物反射回来被雷达接收到的尖形波.由图中所给信息计算障碍物离雷达站的距离.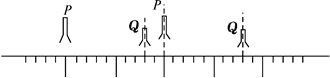
如图所示,有人利用安装在气球载人舱内的单摆来确定气球的高度.已知该单摆在海平面处的周期是T0.当气球停在某一高度时,测得该单摆周期为T.求该气球此时离海平面的高度h.(把地球看做质量均匀分布的半径为R的球体)
如图所示,图中摆长为L的单摆安置在倾角θ的光滑斜面上.此单摆的周期为________.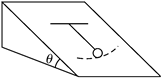
一列横波向右传播,在沿波的传播方向上有相距2.4 m的P、Q两质点,某一时刻它们都处在平衡位置,如图所示,此时,P、Q之间只有一个波峰,则此波的波长可能为多少?