若数列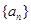
的前n项和为
，则下列命题：
（1）若数列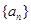是递增数列，则数列
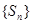也是递增数列；
（2）数列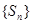是递增数列的充要条件是数列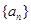的各项均为正数；
（3）若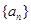是等差数列（公差
），则
的充要条件是
（4）若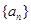是等比数列，则
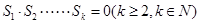的充要条件是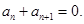
其中，正确命题的个数是（ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
函数y＝e|ln x|－|x－1|的图象大致是( )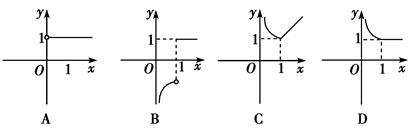
函数y＝f(x)的图象与函数g(x)＝log2x(x＞0)的图象关于原点对称，则f(x)的表达式为( )
| A．f(x)＝(x＞0) | B．f(x)＝log2(－x)(x＜0) |
| C．f(x)＝－log2x(x＞0) | D．f(x)＝－log2(－x)(x＜0) |
函数f(x)的定义域为R，若f(x＋1)与f(x－1)都是奇函数，则( )
| A．f(x)是偶函数 | B．f(x)是奇函数 |
| C．f(x)＝f(x＋2) | D．f(x＋3)是奇函数 |
已知函数f(x)＝，若f(2－a2)＞f(a)，则实数a的取值范围是( )
| A．(－∞，－1)∪(2，＋∞) | B．(－1,2) |
| C．(－2,1) | D．(－∞，－2)∪(1，＋∞) |
设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－2)＝0，则不等式f(x)g(x)>0的解集是( )
| A．(－2,0)∪(2，＋∞) |
| B．(－2,0)∪(0,2) |
| C．(－∞，－2)∪(2，＋∞) |
| D．(－∞，－2)∪(0,2) |