如图所示，真空室内竖直条形区域I存在垂直纸面向外的匀强磁场，条形区域Ⅱ（含I、Ⅱ区域分界面）存在水平向右的匀强电场，电场强度为E，磁场和电场宽度均为l且足够长，M、N为涂有荧光物质的竖直板。现有一束质子从A处连续不断地射入磁场，入射方向与M板成60°夹角且与纸面平行如图。质子束由两部分组成，一部分为速度大小为v的低速质子，另一部分为速度大小为3v的高速质子，当I区中磁场较强时，M板出现两个亮斑，缓慢改变磁场强弱，直至亮斑相继刚好消失为止，此时观察到N板有两个亮斑。已知质子质量为m，电量为e，不计质子重力和相互作用力，求：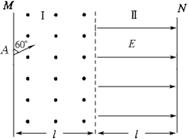
（1）此时I区的磁感应强度；
（2）N板两个亮斑之间的距离。
物体做直线运动，其位移图象如图所示，试求；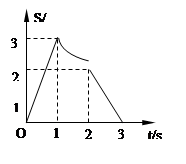
（1）5s末的瞬时速度
（2）20s内的平均速度
（3）第二个10S内的平均速度
（4）30s内的位移
(9分)如图所示，光滑水平轨道上有三个木块A、B、C，质量分别为mA＝3m、mB＝mC＝m，开始时 B、C均静止，A以初速度v0向右运动，A与B碰撞后分开，B又与C发生碰撞并粘在一起，此后A与B间的距离保持不变．求B与C碰撞前B的速度大小．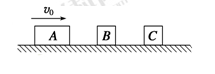
如图所示，为某种透明介质的截面图，△AOC为等腰直角三角形，BC为半径R="12" cm的四分之一圆弧，AB与水平屏幕MN垂直并接触于A点．一束红光射向圆心O，在AB分界面上的入射角i=45o，结果在水平屏幕MN上出现两个亮斑。已知该介质对红光的折射率为n=
，求两个亮斑与A点间的距离。
如图所示，“13”形状的各处连通且粗细相同的细玻璃管竖直放置在水平地面上，只有竖直玻璃管FG中的顶端G开口，并与大气相通，水银面刚好与顶端G平齐。AB =" CD" = L，BD =" DE" =
，FG =
。管内用水银封闭有两部分理想气体，气体1长度为L，气体2长度为L/2，L = 76cm。已知大气压强P0 = 76cmHg，环境温度始终为t0 = 27℃，现在仅对气体1缓慢加热，直到使BD管中的水银恰好降到D点，求此时（计算结果保留三位有效数字）
① 气体2的压强P2为多少厘米汞柱？
② 气体1的温度需加热到多少摄氏度？
如图所示，现有一个小物块，质量为m=80g，带上正电荷q =2
10－4C。与水平的轨道之间的滑动摩擦系数m= 0.2，在一个水平向左的匀强电场中，E = 4103V/m，在水平轨道的末端N处，连接一个光滑的的半圆形轨道，半径为R=40cm，取g = 10m/s2，求： 
（1）若小物块恰能运动到轨道的最高点L，那么小物块应从距N点多远处的A点释放？
（2）如果小物块在上小题中的位置A释放，当它运动到P点（轨道中点）时轨道对它的支持力等于多少？
（3）小物块在位置A释放，当运动到N点时，突然撤去电场，同时加一匀强磁场，磁感应强度
，方向垂直纸面向里，问能否运动到L点？（回答：“能”或“不能”即可）如果小物块最后能落回到水平面MN上，则刚到达MN时小物块的速度大小为多少？