一辆做匀加速直线运动的轿车,以5m/s2的加速度经过路边相距16m的两路标,它经过第一路标时的速度为3m/s,那么经过第二路标时的速度为多少 ?
如图是“神舟”系列航天飞船返回舱返回地面的示意图,假定其过程可简化为:打开降落伞一段时间后,整个装置匀速下降,为确保安全着陆,需点燃返回舱的缓冲火箭,在火箭喷气过程中返回舱做减速直线运动,则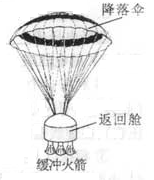
A.火箭开始喷气瞬间伞绳对返回舱的拉力变小
B.返回舱在喷气过程中减速的主要原因是空气阻力
C返回舱在喷气过程中所受合外力可能做正功
D.返回舱在喷气过程中处于失重状态
如图所示,某货场而将质量为m1="100" kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物中轨道顶端无初速滑下,轨道半径R="1.8" m。地面上紧靠轨道次排放两声完全相同的木板A、B,长度均为l=2m,质量均为m2="100" kg,木板上表面与轨道末端相切。货物与木板间的动摩擦因数为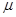 1,木板与地面间的动摩擦因数
1,木板与地面间的动摩擦因数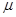 =0.2。(最大静摩擦力与滑动摩擦力大小相等,取g="10" m/s2)
=0.2。(最大静摩擦力与滑动摩擦力大小相等,取g="10" m/s2)
(1)求货物到达圆轨道末端时对轨道的压力。
(2)若货物滑上木板4时,木板不动,而滑上木板B时,木板B开始滑动,求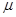 1应满足的条件。
1应满足的条件。
(3)若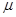 1=0。5,求货物滑到木板A末端时的速度和在木板A上运动的时间。
1=0。5,求货物滑到木板A末端时的速度和在木板A上运动的时间。
一卡车拖挂一相同质量的车厢,在水平直道上以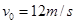 的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为
的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为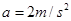 的加速度减速滑行。在车厢脱落
的加速度减速滑行。在车厢脱落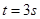 后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
如图,质量 的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经
的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经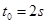 拉至B处。(已知
拉至B处。(已知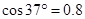 ,
,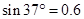 。取
。取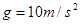 )
)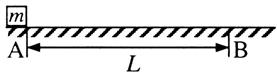
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。
质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s。耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,耙所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变。求:
(1)拖拉机的加速度大小。
(2)拖拉机对连接杆的拉力大小。
(3)时间t内拖拉机对耙做的功。