已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(1)若用数组(x,y,z)中的x,y,z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由.
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 频数 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
已知(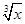 +x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-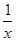 )2n的展开式中:
)2n的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
已知( -
-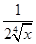 )n的展开式中,前三项系数的绝对值依次成等差数列.
)n的展开式中,前三项系数的绝对值依次成等差数列.
(1)证明:展开式中没有常数项;
(2)求展开式中所有的有理项.
已知(a2+1)n展开式中各项系数之和等于(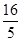 x2+
x2+ )5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项等于54,求a的值.
)5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项等于54,求a的值.