(本小题12分)离心率为 的椭圆
的椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,
, 是坐标原点.
是坐标原点.
(1)求椭圆 的方程;
的方程;
(2)若直线 与
与 交于相异两点
交于相异两点 、
、 ,且
,且


 ,求
,求 .(其中
.(其中 是坐标原点)
是坐标原点)
已知椭圆 .
(1)求椭圆C的离心率;
(2)设
为原点,若点
在直线
,点
在椭圆
上,且
,求线段
长度的最小值.
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: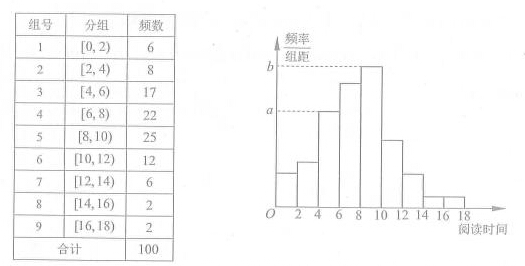
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的
的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
如图,在三棱柱
中,侧棱垂直于底面,
,
,
、
分别为
、
的中点.
(1)求证:平面
平面
;
(2)求证:
平面
;
(3)求三棱锥
的体积.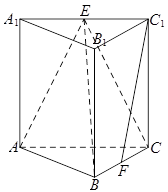
函数
的部分图象如图所示.
(1)写出
的最小正周期及图中
、
的值;
(2)求
在区间
上的最大值和最小值.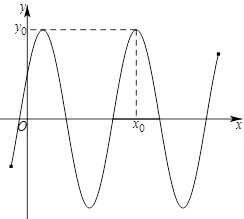
已知
是等差数列,满足
,数列
满足
,且
是等比数列.
(1)求数列
和
的通项公式;
(2)求数列
的前
项和.