如图,AC与BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )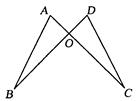
| A.AB=DC; | B.OB=OC; | C.∠A=∠D; | D.∠AOB=∠DOC |
边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. |
B. |
C. |
D. |
正三角形△ABC的边长为3,依次在边AB、BC、CA上取点A1、B1、C1,使AA1=BB1=CC1=1,则△A1B1C1的面积是( )
A.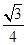 B.
B.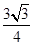 C.
C. D.
D.
如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )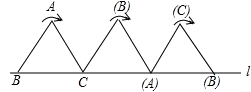
A.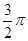 cm cm |
B.(2+ 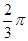 )cm )cm |
C. cm cm |
D.3cm |
如图所示,共有等腰三角形( )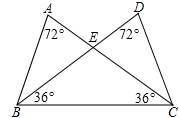
| A.4个 | B.5个 | C.3个 | D.2个 |
如图,△ABC中,BA=BC,∠C=72°,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC交AB于E,则图中的等腰三角形共有( )个.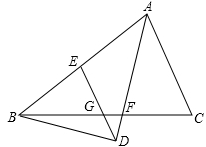
| A.5 | B.6 | C.7 | D.8 |