如图所示,某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在北偏东30°方向处,问B处到灯塔M的距离是多少海里?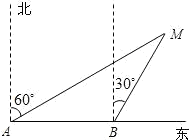
某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成。
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要做多少件夏凉小衫才能完成任务?
如图,⊙O1与⊙O2相交于A、B两点,若AB=O1A=4,O2A=2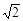 .
.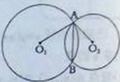
求:(1)∠O1AO2的度数;(2)O1与O2之间的距离。
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.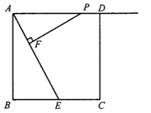
(1)求证:△PFA∽△ABE;
(2)若AP=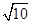 ,求△PFA的面积
,求△PFA的面积
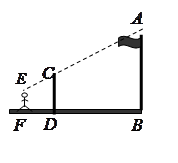
九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度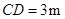 ,标杆与旗杆的水平距离
,标杆与旗杆的水平距离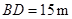 ,人的眼睛与地面的高度
,人的眼睛与地面的高度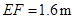 ,人与标杆CD的水平距离
,人与标杆CD的水平距离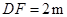 ,求旗杆
,求旗杆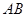 的高度.
的高度.