某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元. 根据市场调查,销售商一次订购量不会超过500件。
(1)设一次订购量为 件,服装的实际出厂单价为
件,服装的实际出厂单价为 元,写出函数
元,写出函数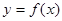 的表达式;
的表达式;
(2)当销售商一次订购了450件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价-成本)
已知存在实数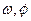 (其中
(其中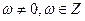 )使得函数
)使得函数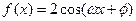 是奇函数,且在
是奇函数,且在 上是增函数。
上是增函数。
(1)试用观察法猜出两组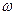 与
与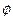 的值,并验证其符合题意;
的值,并验证其符合题意;
(2)求出所有符合题意的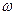 与
与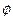 的值。
的值。
已知矩形纸片ABCD中,AB=6 ,AD=12
,AD=12 ,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点,M、N分别位于边AB、BC上,设
,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点,M、N分别位于边AB、BC上,设 。
。
(ⅰ)试将 表示成
表示成 的函数;
的函数;
(ⅱ)求 的最小值。
的最小值。
某港口的水深 (米)是时间
(米)是时间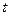 (0≤
(0≤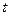 ≤24,单位:小时)的函数,下面是不同时间的水深数据:
≤24,单位:小时)的函数,下面是不同时间的水深数据:
根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成正弦函数 的图像.
的图像.
(1)试根据以上数据,求出 的表达式;
的表达式;
(2)一般情况下,船舶航行时,船底离海底的距离不少于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,则在港内停留的时间最多不能超过多长时间?(忽略进出港所用的时间)?
如图某地夏天从8~14时用电量变化曲线近似满足函数 .
.
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
已知函数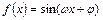 (
( ,
,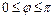 )为偶函数,且其图像上相邻的一个最高点和最低点之间距离为
)为偶函数,且其图像上相邻的一个最高点和最低点之间距离为 .
.
⑴求 的解析式;
的解析式;
⑵若 ,求
,求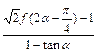 的值。
的值。