设函数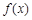 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意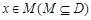 ,有
,有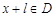 ,且
,且 ,则称
,则称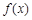 为
为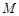 上的“
上的“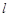 高调函数”.现给出下列命题:
高调函数”.现给出下列命题:
①函数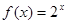 为
为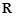 上的“1高调函数”;
上的“1高调函数”;
②函数 为
为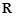 上的“
上的“ 高调函数”;
高调函数”;
③如果定义域为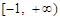 的函数
的函数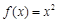 为
为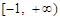 上“
上“ 高调函数”,那么实数
高调函数”,那么实数 的取值范围是
的取值范围是 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
等比数列中,前三项之和为168,其次三项之和为21,则首项为_______________.
在等差数列{an}中,若a10=0,则有a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立,类比上述性质,相应地,在等比数列{an}中,若b9=1,则有等式__________成立.
在等比数列{an}中,已知a7a12=5,则a8a9a10a11=________________.
已知等比数列{an}中,a3=3,a10=384,则该数列的通项an=_____________.
在等差数列{an}中,若a10=0,则有a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立,类比上述性质,相应地,在等比数列{an}中,若b9=1,则有等式______________________成立.