如图10所示,长L=0.20m的丝线的一端栓一质量为m=1.0×10-4Kg带电荷量为
q=+1.0×10-6C的小球,另一端连在一水平轴O上,丝线拉着小球可在竖直平面内做圆周运动,整个装置处在竖直向上的匀强电场中,电场强度E=2.0×103N/C,现将小球拉到与轴O在同一水平面的A点,然后无初速地将小球释放,取g=10m/s2,求(1)小球通过最高点B时速度的大小(2)小球通过最高点时,丝线对小球的拉力大小。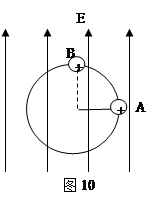
如图所示,物块C质量mc=4kg,上表面光滑,左边有一立柱,放在光滑水平地面上。一轻弹簧左端与立柱连接,右端与物块B连接,mB=2kg;竖直放置的半径R=1.8m的光滑四分之一圆弧最低点的切线水平,且与物块C上表面在同一水平面上。物块A从圆弧的顶点静止释放,达到最低点时炸裂成质量m1=2kg,m2=1kg的两个物块1和2,物块1水平向左运动与B粘合在一起,物块2具有水平向右的速度,刚好回到圆弧的最高点。A、B都可以看着质点。取g="10" m/s2。求:
(1) 物块A炸裂时增加的机械能△E是多少?
(2) 在以后的过程中,弹簧最大的弹性势能Epm是多大?
如图所示是我国某优秀跳水运动员在跳台上腾空而起的英姿。跳台距水面高度为10 m,此时她恰好到达最高位置,估计此时她的重心离跳台台面的高度为1 m。当她下降到手触及水面时要伸直双臂做一个翻掌压水花的动作,这时她的重心离水面也是1 m.g取10 m/s2,求:
(1)从最高点到手触及水面的过程中,其重心的运动可以看作是自由落体运动,她在空中完成一系列动作可利用的时间为多长?
(2)忽略运动员进入水面过程中受力的变化,入水之后,她的重心能下沉到离水面约
2.5m处,试估算水对她的平均阻力约是她自身重力的几倍?
.如图所示,一小球自平台上水平抛出,恰好落在临近平台的一倾角为α =53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8m,g=10m/s2,sin53°=0.8,cos53°=0.6,则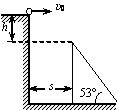
⑴小球水平抛出的初速度υ0是多少?
⑵斜面顶端与平台边缘的水平距离s是多少?
如图所示,AB为1/4圆弧轨道,半径为R=0.8m,BC是水平轨道,长S=3m,BC处的摩擦系数为μ=1/15,今有质量m=1kg的物体,自A点从静止起下滑到C点刚好停止。求: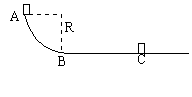
(1)物体在AB段克服阻力所做的功为多少?
(2)物体下滑到B点时对圆弧轨道的压力多大?
一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以2.5m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少;
(2)警车发动后要多长时间才能追上货车.