某家庭为小孩买教育保险,小孩在出生的第一年父母就交纳保险金,数目为a1,以后每年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的保险金数目为a1,a2,…是一个公差为d的等差数列,与此同时保险公司给予优惠的利息政策,不仅采用固定利率,而且计算复利,这就是说,如果固定利率为r(r>0),那么,在第n年末,第一年所交纳的保险金就变为a1(1+r)n-1,第二年所交纳的保险金就变为a2(1+r)n-2,…,以Tn表示到第n年末所累计的保险金总额。
(1)写出Tn与Tn+1的递推关系(n≥1);
(2)若a1=1,d=0.1,求{Tn}的通项公式。(用r表示)
已知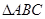 中,角
中,角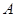 、
、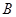 、
、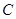 的对边分别为
的对边分别为 、
、 、
、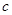 ,
,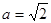 ,向量
,向量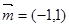 ,
,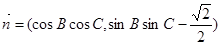 ,且
,且 .
.
(Ⅰ)求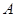 ;
;
(Ⅱ)当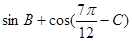 取得最大值时,求
取得最大值时,求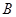 和
和 .
.
已知 菱形
菱形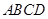 所在平面,点
所在平面,点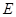 、
、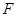 分别为线段
分别为线段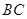 、
、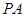 的中点.
的中点.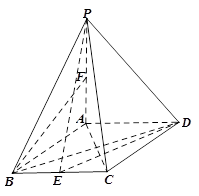
(Ⅰ)求证: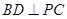 ;
;
(Ⅱ)求证: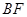 ∥平面
∥平面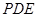 .
.
(本小题满分13分)若存在实常数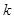 和
和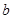 ,使得函数
,使得函数 和
和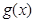 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: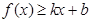 和
和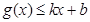 ,则称直线
,则称直线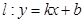 为
为 和
和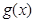 的“隔离直线”.已知
的“隔离直线”.已知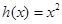 ,
,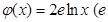 为自然对数的底数).
为自然对数的底数).
(1)求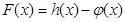 的极值;
的极值;
(2)函数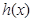 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
(本小题满分13分)已知等比数列{an}的公比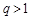 ,前n项和为Sn,S3=7,且
,前n项和为Sn,S3=7,且 ,
, ,
,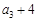 成等差数列,数列{bn}的前n项和为Tn,
成等差数列,数列{bn}的前n项和为Tn, ,其中
,其中 N*.
N*.
(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式;
(3)设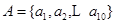 ,
,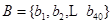 ,
,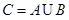 ,求集合C中所有元素之和.
,求集合C中所有元素之和.
(本小题满分13分)已知圆C的方程为: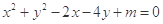
(1)求 的取值范围;
的取值范围;
(2)若圆C与直线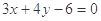 交于M、N两点,且
交于M、N两点,且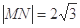 ,求
,求 的值.
的值.
(3)设直线 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得以
,使得以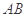 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.