如图所示，一传热性能良好的容器两端是直径不同的两个圆筒，里面各有一个活塞A、B，其横截面积分别为SA=10cm2、SB=4cm2，质量分别为mA=6kg、mB=4kg，它们之间用一质量不计的硬质细杆相连，两活塞均可以在圆筒中无摩擦滑动但不漏气，在气温为－23℃时，用销子M把B锁住，打开阀门K，使容器和大气相通，随后关闭K，此时容器中气体体积为300cm3，当气温升高27℃时，把销子M拔去但不漏气，设大气压始终为105Pa，容器内温度始终和外界相同．求：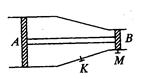
（1）销子拔去时，两活塞的加速度；
（2）活塞在各自圆筒范围内运动一段多大距离后，速度达到最大值？
一定质量的理想气体经历了温度缓慢升高的变化，如图所示，p—T和V—T图各记录了其部分变化过程，试求：
①温度600K时气体的压强．
②在p-T图象上将温度从400K升高到600K
的变化过程补充完整．
如图a所示的平面坐标系xOy，在整个区域内充满了匀强磁场，磁场方向垂直坐标平面，磁感应强度B随时间变化的关系如图b所示，开始时刻，磁场方向垂直纸面向里(如图)。t=0时刻，有一带正电的粒子(不计重力)从坐标原点O沿x轴正向进入磁场，初速度为v0=2´103m/s。已知正粒子的比荷为1.0´104C/kg，其它有关数据见图中标示（磁感应强度B取垂直纸面向里为正）。试求：
(1)t=
´10-4s时刻，粒子的坐标。
(2)粒子从开始时刻起经多长时间第一次到达y轴。
(3)粒子是否还可以返回坐标原点O？如果可以，则经多长时间第一次返回坐标原点O？
某学校学生进行“交通信号灯”的课题研究中发现在公路的十字路口, 红灯拦停了很多汽车。 若拦停的汽车排成笔直的一列, 最前面的一辆汽车的前端刚好与路口停车线相齐, 相邻两车的前端之间的距离均为L =" 6.0" m,若汽车起动时都以a =2.5m/s2 的加速度作匀加速运动, 加速到v="10.0" m/s 后做匀速运动通过路口。该路口亮绿灯时间t =" 40.0" s, 而且有按倒计时显示的时间显示灯. 另外交通规则规定: 原在绿灯时通行的汽车, 红灯亮起时, 车头已越过停车线的汽车允许通过。求：若绿灯亮起瞬时, 所有司机同时起动汽车, 问有多少辆汽车能通过路口？
光滑水平面上有一质量为M滑块，滑块的左侧是一光滑的圆弧，圆弧半径为R="l.0" m。一质量为m的小球以速度v0。向右运动冲上滑块。已知M= 4m，g取l0m/s2，若小球刚好没跃出
圆弧的上端，求：
①小球的初速度v0是多少?
②滑块获得的最大速度是多少?
半径为R的
透明圆柱体固定于地面上，透明体对红光的折射率为n=
如图所示。今让一束平行于地面的红光射向圆柱体左侧，经折射红光照射到右侧地面上。完成光路图，并求圆柱体右侧地面上的黑暗部分长度。