下表是火星和地球部分数据对照表,把火星和地球视为质量均匀的理想球体,它们绕太阳的运动近似看作匀速圆周运动,从表中数据可以分析得出
| |
质量(千克) |
公转周期(天) |
自转周期 (小时) |
近似公转轨道半径(米) |
星球半径(米) |
| 火星 |
6.421×1023 |
686.98 |
24.62 |
2.28×1011 |
3.395×106 |
| 地球 |
5.976×1024 |
365.26 |
23.93 |
1.50×1011 |
6.378×106 |
A.地球所受向心力较大
B.地球公转的动能较小
C.火星两极处地表重力加速度较大
D.火星的第一宇宙速度较大
下列说法正确的是()
| A.牛顿总结出了万有引力定律并测出了万有引力常量 |
| B.法拉第发现了电磁感应现象 |
| C.光电效应现象说明光具有粒子性 |
| D.太阳辐射的能量主要来自太阳内部的核裂变反应 |
如图,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b。a球质量为m,静置于地面;b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧。从静止开始释放b后,a可能达到的最大高度为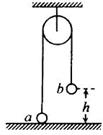
| A.h | B.l.5h |
| C.2h | D.2.5h |
一物体静止在升降机的地板上,在升降机加速上升的过程中,地板对物体的支持力所做的功等于
| A.物体重力势能的增加量 |
| B.物体动能的增加量 |
| C.物体动能的增加量加上物体重力势能的增加量 |
| D.物体动能的增加量减去物体重力势能的增加量 |
铁路提速要解决许多具体的技术问题,其中提高机车牵引功率是一个重要问题。已知匀速行驶时,列车所受阻力与速度的平方成正比,即f=kv2。列车要提速,就必须研制出更大功率的机车,那么当列车分别以120Km/h和40Km/h的速度在水平轨道上匀速行驶时,机车的牵引功率之比为
| A.3:1 | B.9:1 | C.27:1 | D.81:1 |
竖直上抛一球,球又落回原处,已知空气阻力的大小正比于球的速度,则
| A.上升过程中克服重力做的功大于下降过程中重力做的功 |
| B.上升过程中克服重力做的功等于下降过程中重力做的功 |
| C.上升过程中克服重力做功的平均功率大于下降过程重力的平均功率 |
| D.上升过程中克服重力做功的平均功率等于下降过程重力的平均功率 |