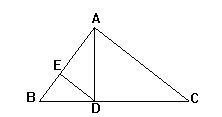
如图,已知直角△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.求∠ADE的度数.
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)每件衬衫降价多少元时,商场平均每天赢利最多?
如图,四边形ABCD是菱形,对角线AC=8 cm , BD=6 cm, DH⊥AB于H,求:DH的长
从旗杆的顶端系一条绳子,垂到地面还多2米,小敏拉起绳子下端绷紧,刚好接触地面,发现绳子下端距离旗杆底部8米,小敏马上计算出旗杆的高度,你知道她是如何解的吗?
已知关于x的方程x2+kx-2=0的一个解与方程 解相同.
解相同.
(1)求k的值;(2)求方程x2+kx-2=0的另一个根.
已知: