科学家发现太空中的γ射线一般都是从很远的星体放射出来的。当γ射线爆发时，在数秒时间内产生的能量相当于太阳在过去100亿年内所能释放的能量的总和。科学家利用超级计算机对γ射线的状态进行了模拟，发现γ射线爆发是起源于一个垂死的星球的“塌缩”过程，只有星球“塌缩”时，才可以释放这么巨大的能量。已知太阳光照射到地球上大约需要8分20秒的时间，由此估算在宇宙中，一次γ射线爆发所释放的能量。（万有引力常量为6.67×10-11 N·m2/kg2，1年按365天算）
(6分)人拉原来静止的重300N的车在水平路面上前进,拉力大小为20N,方向斜向上且与水平方向成300角,车前进500米,车与路面的动摩擦因数为0.03,求:
(1)拉力对车所做的功;
(2)摩擦力对车所做的功;
(3)车获得的动能.
如图所示，P、Q为水平面内平行放置的光滑金属长直导轨，间距为L1，处在竖直向下、磁感应强度大小为B1的匀强磁场中，一导体杆ef垂直于P、Q放在导轨上，在外力作用下向左做匀速直线运动．质量为m、每边电阻均为r、边长为L2的正方形金属框abcd置于竖直平面内，两顶点a、b通过细导线与导轨相连，磁感应强度大小为B2的匀强磁场垂直金属框向里，金属框恰好处于静止状态，不计其余电阻和细导线对a、b点的作用力．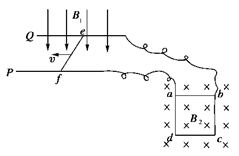
(1)通过ab边的电流Iab是多大？
(2)导体杆ef的运动速度v是多大？
在距某村庄较远的地方修建了一座小型水电站，发电机输出功率为9kW，输出电压为500V，输电线的总电阻为10Ω，允许线路损耗的功率为发电机输出功率的4%，求：
(1)村民和村办小企业需要220V电压时，所用升压变压器和降压变压器的原、副线圈的匝数比各为多少？(不计变压器的损耗)
(2)若不用变压器而由发电机直接输送，村民和村办小企业得到的电压和功率是多少？
(10分)如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m、导轨平面与水平面成θ＝37°角，下端连接阻值为R的电阻，匀强磁场方向与导轨平面垂直．质量为0.2kg，电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为0.25.
(1)求金属棒沿导轨由静止开始下滑时的加速度大小．
(2)当金属棒下滑速度达到稳定时，电阻R消耗的功率为8W，求该速度的大小．
(3)在上问中，若R＝2Ω，金属棒中的电流方向由a到b，求磁感应强度的大小与方向(g＝10m/s2，sin37°＝0.6，cos37°＝0.8)
如图所示，在绝缘水平面上，相距为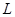
的
、
两点处分别固定着两个等量正电荷，a、b是
连线上两点，其中
=
=
,
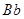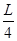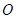为连线中点。一质量为
带电量为+
的小滑块(可视为质点)以初动能
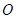从a点出发，沿直线向b点运动,其中小滑块第一次经过点时的动能为初动能的
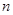倍(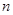>1)，到达b点时动能恰好为零，小滑块最终停在点，求
(1)小滑块与水平面间的动摩擦因数
；
(2)
两点间的电势差
；
(3)小滑块运动的总路程s.，