如图所示,A、B两木块质量均为1kg, A与B、B与墙面之间的动摩擦因数均为0.1 .若A、B的初速度为零,当水平力F取不同值时,关于A、B之间的摩擦力f1,B与墙壁之间的摩擦力f2的大小,下列说法中正确的是(g=10m/s2):( 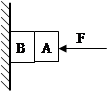
A.F=300N时,f1=30N, f2=30N
B.F=300N时,f1=10N, f2=20N
C.F=100N时,f1=10N, f2=10N
D.F=100N时,f1=5N, f2=10N
作用于O点的五个恒力F1、F2、F3、F4、F5的矢量图的末端跟O点恰好构成一个正六边形,如图示.已知这五个恒力中的最大力F3=10N,则这五个力的合力的大小是()
| A.0 | B.10N | C.20N | D.30N |
同一平面内的三个力,大小分别为4N、6N、7N,若三力同时作用于某一物体,则该物体所受三力合力的最大值和最小值分别为()
| A.17N、3N | B.17N、0 |
| C.9N、0 | D.5N、3N |
下列关于弹力的说法中,错误的是()
| A.只要两个物体接触就一定能产生弹力 |
| B.压力、支持力的方向总是垂直于支持面的 |
| C.平时我们说的拉力、支持力、压力、推力等都是弹力 |
| D.两个接触并发生弹性形变的物体间一定产生弹力 |
水平桌面上放一重100牛的物体,与桌面间的滑动摩擦系数为0.2,当依次用15N,30N的水平拉力拉这个物体时,物体受到的摩擦力依次为:(设最大静摩擦力等于滑动摩擦力)()
| A.15N,30N | B.15N,20N |
| C.10N,30N | D.15N,30N |
如图所示,在水平面上有一个向右运动的物体,物体的质量为20kg,与水平面间的动摩擦因数为0.1,它在运动过程中还受到一个水平向左的大小为10N的拉力作用,则物体所受滑动摩擦力的大小为()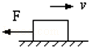
| A.10N,水平向右 | B.10N,水平向左 |
| C.20N,水平向右 | D.20N,水平向左 |