某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
| 捐款(元) |
1 |
 2 2 |
3 |
4 |
| 人数 |
6 |
|
|
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组( )
A.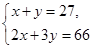 B.
B.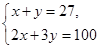 C.
C.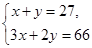 D.
D.
(2)(2005年,乌鲁木齐)为满足市民对优质教育的需求,某中学决定改变办学条件,计划拆除一部分旧校舍、建造新校舍.拆除旧校舍每平方米需80元,建造新校舍每平方米需700元.计划在年内拆除旧校舍与建造新校舍共7200平方米,在实施中为扩大绿地面积,新建校舍只完成了计划的80%,而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.
①求原计划拆、建面积各是多少平方米?
②若绿化1平方米需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?